系列文章目录及链接
上篇:机器学习(五) -- 监督学习(4) -- 集成学习方法 - 随机森林
下篇:
前言
tips:标题前有“***”的内容为补充内容,是给好奇心重的宝宝看的,可自行跳过。文章内容被“文章内容”删除线标记的,也可以自行跳过。“!!!”一般需要特别注意或者容易出错的地方。
本系列文章是作者边学习边总结的,内容有不对的地方还请多多指正,同时本系列文章会不断完善,每篇文章不定时会有修改。
由于作者时间不算富裕,有些内容的《算法实现》部分暂未完善,以后有时间再来补充。见谅!
文中为方便理解,会将接口在用到的时候才导入,实际中应在文件开始统一导入。
一、线性回归通俗理解及定义
1、什么叫线性回归(What)
线性回归(Linear Regression)简单来讲,就是用一条直线尽量去“拟合”一组数据。求得的这条直线(模型),可以用于预测其他未出现的数据。
1.1、***一些性质
咱把“线性回归”拆分一下,拆成“线性”、“回归”,这里的“线性”是一类模型,“线性模型”;“回归”是一类问题,“回归问题”,这样“线性回归”就可以是“用线性模型来解决回归问题”。
以下为一些概率性质:
线性(线性关系):指量与量之间按比例、呈直线关系。
非线性:不按比例、不呈直线关系。
简单理解线性就是里面的变量都是一次的,即n元一次方程,非线性就是可以高于一次的。
线性关系和线性模型:线性关系一定是线性模型,线性模型不一定是线性关系。(线性模型可以是非线性的)
回归:回归问题(回归分析),建立一个数学模型来描述因变量和自变量之间的关系。和分类分析是相对的,预测结果是连续的。(数学上叫自变量、因变量,机器学习上叫特征值、目标值)
分类:预测结果是离散的。
拟合:就是把平面上一系列的点,用一条光滑的曲线连接起来。
请结合【机器学习(四) -- 模型评估(1)一.3】理解过拟合和欠拟合
尽量拟合就是可以有一定误差,不一定要每个点都经过,这和“过拟合”有关。
2、线性回归的目的(Why)
核心思想:找到一条拟合数据的直线。
(如直线是y=wx+b,x是特征值,y是目标值,我们就是要求出一组w和b。)
回归问题:前面说过,可以简单的把回归问题和分类问题区分为:回归问题的预测结果是连续的,分类问题的预测结果是离散的。
***回归问题来源:英国科学家高尔顿(Galton)在研究身高的遗传关系时发现了一种“趋中效应”:
父亲高于平均身高时,其儿子的身高比他更高的概率要小于比他更矮的概率;
父亲矮于平均身高时,其儿子的身高比他更矮的概率要小于比他更高的概率。
简单来说就是身高回归平均值。“回归”一词也就是这么来的。
3、如何找这条线(How)
线性回归流程:
- 随机画一条直线,作为初始的直线
- 检查一下它的拟合效果,
- 如果不是最好的(达到阈值),就调整直线位置和角度
- 重复第2、3步,直到最好效果(到达设定的阈值),最终就是我们想要的模型。
其中有两个问题:如何检查模型拟合效果?如何调整模型位置角度?
针对检查模型拟合效果,我们一般比较预测值与真实值之间的差值(均方误差,MSE)——最小二乘问题
针对调整模型位置角度,我们采用——梯度下降法
最小二乘问题:这是一个最优化问题,误差是不可避免的,我们要使总的误差尽可能的小。把每一个预测值减去真实值的平方相加,在除以数据量,我们要使这个值最小。
梯度下降法:也叫最速下降法。梯度(函数增长速度最快的方向/方向导数取最大值的方向)。
形象的理解是你站在山上,想要用最快的方式下山,当然是那里最陡,朝哪走最快, ,在数学中就是导数啦,在一个3维立体图中,我们应该朝着当前点梯度的反方向前进。
,在数学中就是导数啦,在一个3维立体图中,我们应该朝着当前点梯度的反方向前进。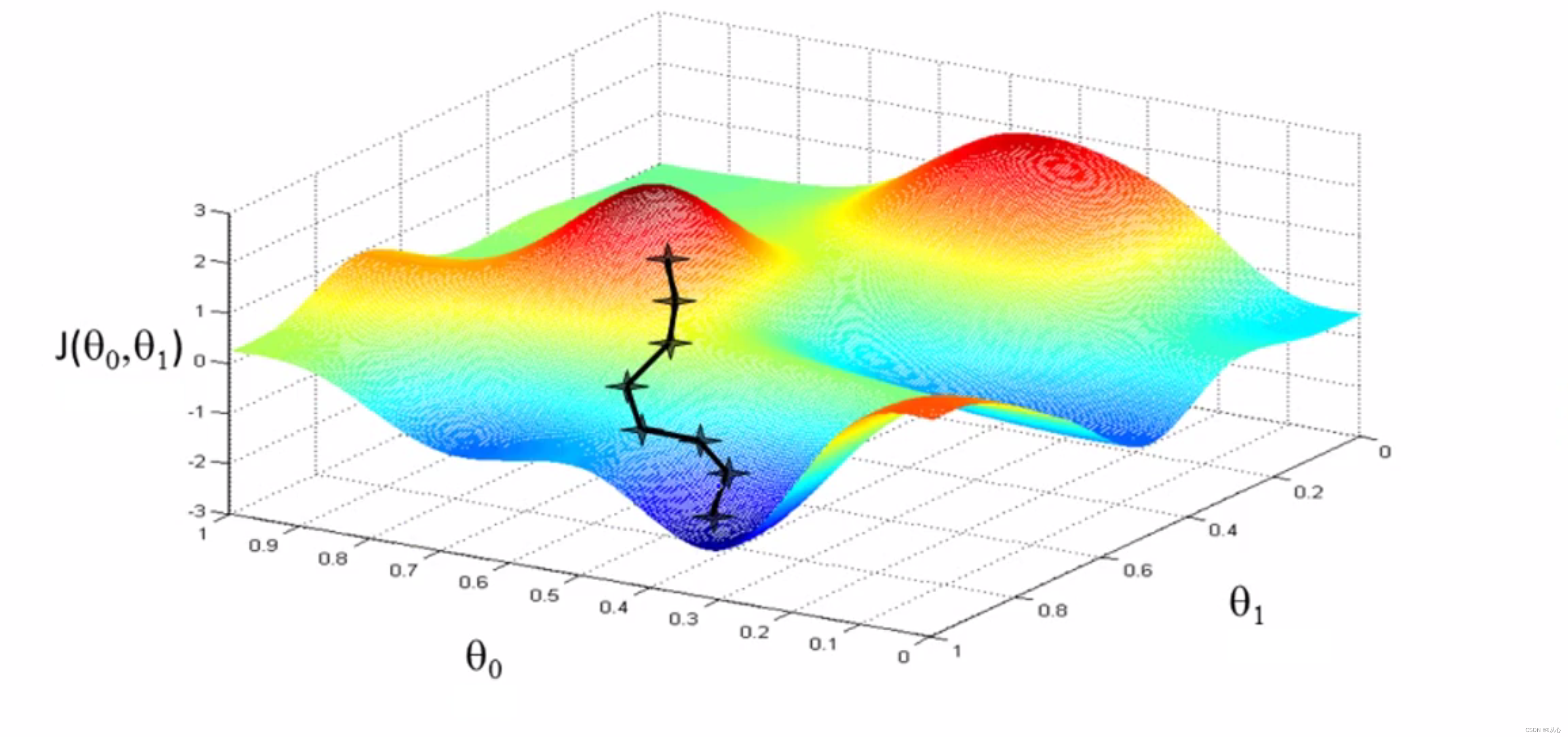 当然也不是随便走多远的,万一你天生神力,从山的一边跳到了另一座山更高的地方也是不行的(步长问题),
当然也不是随便走多远的,万一你天生神力,从山的一边跳到了另一座山更高的地方也是不行的(步长问题), ,步子太大就容易跳过最优解,甚至使误差逐渐变得更大,步长太小又会使下山(找到最优解)的速度变得极慢。
,步子太大就容易跳过最优解,甚至使误差逐渐变得更大,步长太小又会使下山(找到最优解)的速度变得极慢。
二、原理理解及公式
和我们切身相关的线性回归例子就是:学科成绩=50%*平时成绩+50%*考试成绩。(在此祝愿小伙伴们,有考试的每门课都是55开,555,37开的哭了QwQ),
最常接触应该是房价预测问题,房子价格=0.02*中心区域的距离+0.04*城市一氧化碳浓度+0.12*自住房平均价格+0.254*城镇犯罪率
线性回归分为单变量线性回归和多变量(多元)线性回归哟,(简单来说,就是一元一次方程和n元一次方程的区别)
1、单变量线性回归
(Linear Regression with One Variable)
先用单变量线性回归来讲,按照上面的步骤咱一步一步来:
1.1、定义模型
(这里需要严谨一点了,f(x)是模型预测值,y是真实值,前一种更形象,但为了便于矩阵计算,后一种更常用)
1.2、目标函数
最小二乘法:使用均方误差(MSE)来判定距离,应该使所有观察值的残差平方和达到最小,即代价函数(cost function)采用平方损失函数用的是,则代价函数为
(!!!这里乘了个1/2是为了后面计算方便。)
然后我们就得到了目标函数(objective function):
结合之后通过调整参数使模型更加贴合真实数据:
(arg min:(argument of the minimum)最小值的参数)
***补充:残差平方和(RSS):等同于SSE(误差项平方和),实际值与预测值之间差的平方之和。
均方误差(MSE):是RSS的的期望值(或均值),(就是乘了个1/m)
***补充:损失函数:是定义在单个样本上的,单个样本的误差。
代价函数:是定义在整个训练集上的,是所有样本误差的平均,也就是损失函数的平均(让代价函数最小)。(有时,也可以认为损失函数就是代价函数)
目标函数:最终需要优化的函数,等于经验风险+结构风险(也就是代价函数 + 正则化项,正则项在后面才会用到)。
1.3、参数估计
求w、b使代价函数最小化的过程,称线性回归模型的最小二乘“参数估计”(parameter estimation)。
1.3.1、梯度下降法
梯度下降法(Gradient Descent,GD):前面也说过梯度是函数增长速度最快的方向/方向导数取最大值的方向,而梯度下降就是要沿着梯度的反方向调整参数,还记得梯度公式吧,梯度是个向量,后面那杂七杂八的一堆是我之前做的笔记,看前面就行。
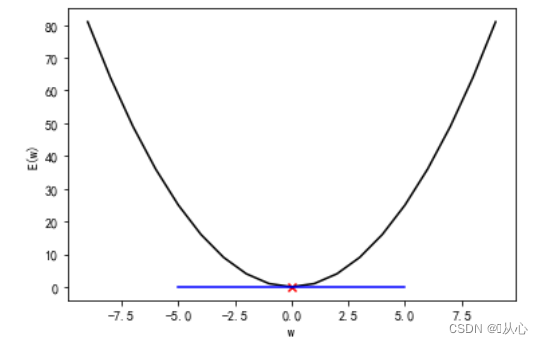
多维的有点复杂,我们用如下的一个简单例子来理解如何进行梯度下降,我们假设横坐标是参数,纵坐标为均方误差,红色标记为初始参数,蓝色为其导数,从上面的公式可以看出梯度就是各个方向的偏导数组成的变量,在这个单变量的例子中梯度可以简单理解成就是其导数。
在此例子中,函数曲线为y=x^2,初始参数为w=7,其导数为-14,显然我们要进行梯度下降,就应该向梯度相反方向调整参数,即向右边移动,向导数相反方向移动,是不是就可以用原参数减去导数即可,这里有一个步长问题,上面也说过,所以为了控制步长(在机器学习中称为学习率)要用原参数减去学习率乘以导数,本例中的公式表达就是这个样子:
关于α(学习率)一般需要手动设置,学习率太小,学习太慢;学习率太大,可能无法收敛,甚至发散;常考虑0.001、0.003、0.01、0.03、0.1、0.3、1、3、10。
***一个小特点:当接近局部最低点时,梯度下降法会自动采用更小幅度(因为导数在变化)。
好了我们知道了他的原来,带回原模型得到的参数更新表达式如下:
(为了同步实现更新,需要如上进行参数传递)
将代价函数代入得到(这里其实吧1/m去掉问题也不大,反正α是手动设置,把α设置成原来的mα是一样的意思):
!!!注意:有的教材可能得到的是如下,这里两者都是正确的哈,只是因为因为在损失函数中f(w,b)和y的相减位置不同导致的。
还有这种表达方式(简单理解,“ := ”就是将左边赋值给右边):
2、多变量(多元)线性回归
多变量(多元)线性回归(Linear Regression with Multiple Variable):也叫多重回归(多变量)。其实只是一个特征值变成了多个特征值的情况。
(!!!注意:多变量时往往要进行特征缩放,因为保持相近的梯度,有助于梯度下降算法快速收敛)
2.1、定义模型
多个特征,模型可以用向量表示
也有这种表示(b=w0,x0=1):
2.2、目标函数
损失函数:
目标函数:
2.3、参数估计
多变量线性回归的参数更新表达式如下:
梯度下降法的缺点 :刚才的例子只是一个最简单的例子,但在实际情况中往往不是,如下图梯度下降法容易陷入局部最优解:
所以实际应用中往往采用其他方法。
2.3.1、随机梯度下降法
随机梯度下降法(Stochastic Gradient Descent,SGD)选择随机一个训练数据,并使用它来更新参数。参数更新表达式变为(1/m去掉了,为了简便一点):
***注意:因为是随机的一个数字,这里的上标不是i了,而是随机数k,(又get一个小细节,哦耶)。
优点:最速下降法更新 1 次参数的时间,随机梯度下降法可以更新 n 次。
随机梯度下降法由于训练数据是随机选择的,更新参数时使用的又是选择数据时的梯度,所以不容易陷入目标函数的局部最优解。
2.3.2、批量梯度下降法
批量梯度下降法(Mini-batch gradient descent,小批量梯度下降算法):类似,只是数据不是全部也不是一个,而是一小部分,参数更新表达式变为
还有随机平均梯度下降算法(Stochastic average gradient descent)
2.3.3、正规方程
梯度下降法是对代价函数的每个参数求偏导,通过迭代算法一步步更新,直到收敛到全局最小值,从而得到最优参数。正规方程是一次性求得最优解。
思想是对于一个简单函数,对参数求导,将其值直接设置为0,就得到参数的值。如下图:
通过求解方程 来找出使得代价函数最小的参数的,(这里用θ更好表示所有参数)
来找出使得代价函数最小的参数的,(这里用θ更好表示所有参数)
***推导过程:
正规方程的优点:
1、不需要学习率α
2、一次计算即可,不用多次迭代
正规方程的缺点:
1、需要计算 ,如果特征数量较大,运算代价大矩阵逆的时间复杂度为 O(n^3) ,通常小于10000可以接受。
,如果特征数量较大,运算代价大矩阵逆的时间复杂度为 O(n^3) ,通常小于10000可以接受。
2、只适用于线性模型
3、多项式回归
多项式回归(高次项):线性回归不适用所有数据,有时需要曲线来适应数据。
(多项式回归时,特征缩放也是很有必要的。)
定义模型:
其他步骤也是类似。
4、正则化
在解决回归过拟合中,我们选择正则化来防止过拟合。
4.1、定义
在学习的时候,数据提供的特征有些影响模型复杂度或者这个特征的数据点异常较多,所以算法在学习的时候尽量减少这个特征的影响(甚至删除某个特征的影响),这就是正则化。
注:调整时候,算法并不知道某个特征影响,而是去调整参数得出优化的结果
4.2、类别
L2正则化
作用:可以使得其中一些W的都很小,都接近于0,削弱某个特征的影响
优点:越小的参数说明模型越简单,越简单的模型则越不容易产生过拟合现象
Ridge回归
L1正则化
作用:可以使得其中一些W的值直接为0,删除这个特征的影响
LASSO回归
5、维灾难(维数灾难)
5.1、定义
随着维度的增加,分类器性能逐步上升,到达某点之后,其性能便逐渐下降
(随着维度(特征数量)的增加,分类器的性能却下降了)
5.2、维数灾难与过拟合
一个栗子
我们假设猫和狗图片的数量是有限的(样本数量总是有限的),假设有10张图片,接下来我们就用这仅有的10张图片来训练我们的分类器。
增加一个特征,比如绿色,这样特征维数扩展到了2维:
增加一个特征后,我们依然无法找到一条简单的直线将它们有效分类
再增加一个特征,比如蓝色,扩展到3维特征空间:
在3维特征空间中,我们很容易找到一个分类平面,能够在训练集上有效的将猫和狗进行分类:
在高维空间中,我们似乎能得到更优的分类器性能。
从1维到3维,给我们的感觉是:维数越高,分类性能越优。然而,维数过高将导致一定的问题:在一维特征空间下,我们假设一个维度的宽度为5个单位,这样样本密度为10/5=2;在2维特征空间下,10个样本所分布的空间大小25,这样样本密度为10/25=0.4;在3维特征空间下,10个样本分布的空间大小为125,样本密度就为10/125=0.08.
如果继续增加特征数量,随着维度的增加,样本将变得越来越稀疏(样本密度变小),在这种情况下,也更容易找到一个超平面将目标分开。然而,如果我们将高维空间向低维空间投影,高维空间隐藏的问题将会显现出来:
过多的特征导致的过拟合现象:训练集上表现良好,但是对新数据缺乏泛化能力。
高维空间训练形成的线性分类器,相当于在低维空间的一个复杂的非线性分类器,这种分类器过多的强调了训练集的准确率甚至于对一些错误or异常的数据也进行了学习,而正确的数据却无法覆盖整个特征空间。为此,这样得到的分类器在对新数据进行预测时将会出现错误。这种现象称之为过拟合,同时也是维灾难的直接体现。
简单的线性分类器在训练数据上的表现不如非线性分类器,但由于线性分类器的学习过程中对噪声没有对非线性分类器敏感,因此对新数据具备更优的泛化能力。换句话说,通过使用更少的特征,避免了维数灾难的发生(也即避免了高维情况下的过拟合)
由于高维而带来的数据稀疏性问题:假设有一个特征,它的取值范围D在0到1之间均匀分布,并且对狗和猫来说其值都是唯一的,我们现在利用这个特征来设计分类器。如果我们的训练数据覆盖了取值范围的20%(e.g 0到0.2),那么所使用的训练数据就占总样本量的20%。上升到二维情况下,覆盖二维特征空间20%的面积,则需要在每个维度上取得45%的取值范围。在三维情况下,要覆盖特征空间20%的体积,则需要在每个维度上取得58%的取值范围... 在维度接近一定程度时,要取得同样的训练样本数量,则几乎要在每个维度上取得接近100%的取值范围,或者增加总样本数量,但样本数量也总是有限的。
如果一直增加特征维数,由于样本分布越来越稀疏,如果要避免过拟合的出现,就不得不持续增加样本数量。
数据在高维空间的中心比在边缘区域具备更大的稀疏性,数据更倾向于分布在空间的边缘区域:
不属于单位圆的训练样本比搜索空间的中心更接近搜索空间的角点。这些样本很难分类,因为它们的特征值差别很大(例如,单位正方形的对角的样本)。
一个有趣的问题是,当我们增加特征空间的维度时,圆(超球面)的体积如何相对于正方形(超立方体)的体积发生变化。尺寸d的单位超立方体的体积总是1 ^ d = 1.尺寸d和半径0.5的内切超球体的体积可以计算为:
在高维空间中,大多数训练数据驻留在定义特征空间的超立方体的角落中。如前所述,特征空间角落中的实例比围绕超球体质心的实例难以分类。
在高维空间中,大多数训练数据驻留在定义特征空间的超立方体的角落中。如前所述,特征空间角落中的实例比围绕超球体质心的实例难以分类:
an 8D hypercube which has 2^8 = 256 corners
事实证明,许多事物在高维空间中表现得非常不同。 例如,如果你选择一个单位平方(1×1平方)的随机点,它将只有大约0.4%的机会位于小于0.001的边界(换句话说,随机点将沿任何维度“极端”这是非常不可能的)。 但是在一个10000维单位超立方体(1×1×1立方体,有1万个1)中,这个概率大于99.999999%。 高维超立方体中的大部分点都非常靠近边界。更难区分的是:如果你在一个单位正方形中随机抽取两个点,这两个点之间的距离平均约为0.52。如果在单位三维立方体中选取两个随机点,则平均距离将大致为0.66。但是在一个100万维的超立方体中随机抽取两点呢?那么平均距离将是大约408.25(大约1,000,000 / 6)!
非常违反直觉:当两个点位于相同的单位超立方体内时,两点如何分离?这个事实意味着高维数据集有可能非常稀疏:大多数训练实例可能彼此远离。当然,这也意味着一个新实例可能离任何训练实例都很远,这使得预测的可信度表现得比在低维度数据中要来的差。训练集的维度越多,过度拟合的风险就越大。
理论上讲,维度灾难的一个解决方案可能是增加训练集的大小以达到足够密度的训练实例。 不幸的是,在实践中,达到给定密度所需的训练实例的数量随着维度的数量呈指数增长。 如果只有100个特征(比MNIST问题少得多),那么为了使训练实例的平均值在0.1以内,需要比可观察宇宙中的原子更多的训练实例,假设它们在所有维度上均匀分布。
对于8维超立方体,大约98%的数据集中在其256个角上。结果,当特征空间的维度达到无穷大时,从采样点到质心的最小和最大欧几里得距离的差与最小距离本身只比趋于零:
距离测量开始失去其在高维空间中测量的有效性,由于分类器取决于这些距离测量,因此在较低维空间中分类通常更容易,其中较少特征用于描述感兴趣对象。
如果理论无限数量的训练样本可用,则维度的诅咒不适用,我们可以简单地使用无数个特征来获得完美的分类。训练数据的大小越小,应使用的功能就越少。如果N个训练样本足以覆盖单位区间大小的1D特征空间,则需要N ^ 2个样本来覆盖具有相同密度的2D特征空间,并且在3D特征空间中需要N ^ 3个样本。换句话说,所需的训练实例数量随着使用的维度数量呈指数增长。
6、正则化线性模型
6.1、Ridge Regression (岭回归、Tikhonov regularization)
岭回归是线性回归的正则化版本,即在原来的线性回归的 cost function 中添加正则项(regularization term):
以达到在拟合数据的同时,使模型权重尽可能小的目的,岭回归代价函数:
α=0:岭回归退化为线性回归
6.2、Lasso Regression(Lasso回归)
Lasso 回归是线性回归的另一种正则化版本,正则项为权L1范数。
【注意 】
- Lasso Regression 的代价函数在 θi=0处是不可导的.
- 解决方法:在θi=0处用一个次梯度向量(subgradient vector)代替梯度,如下式
- Lasso Regression 的次梯度向量
Lasso Regression 有一个很重要的性质是:倾向于完全消除不重要的权重。
例如:当α 取值相对较大时,高阶多项式退化为二次甚至是线性:高阶多项式特征的权重被置为0。
也就是说,Lasso Regression 能够自动进行特征选择,并输出一个稀疏模型(只有少数特征的权重是非零的)。
6.3、Elastic Net (弹性网络)
弹性网络在岭回归和Lasso回归中进行了折中,通过 混合比(mix ratio) r 进行控制:
- r=0:弹性网络变为岭回归
- r=1:弹性网络便为Lasso回归
弹性网络的代价函数 :
一般来说,我们应避免使用朴素线性回归,而应对模型进行一定的正则化处理,那如何选择正则化方法呢?
小结:
-
常用:岭回归
-
假设只有少部分特征是有用的:
- 弹性网络
- Lasso
- 一般来说,弹性网络的使用更为广泛。因为在特征维度高于训练样本数,或者特征是强相关的情况下,Lasso回归的表现不太稳定。
API
from sklearn.linear_model import Ridge, ElasticNet, Lasso
6.4、Early Stopping (了解)
Early Stopping 也是正则化迭代学习的方法之一。
其做法为:在验证错误率达到最小值的时候停止训练。
旧梦可以重温,且看:机器学习(五) -- 监督学习(4) -- 集成学习方法 - 随机森林
欲知后事如何,且看:
-



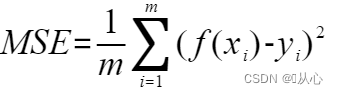














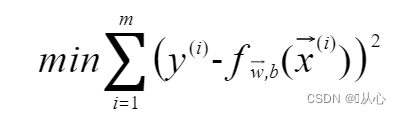
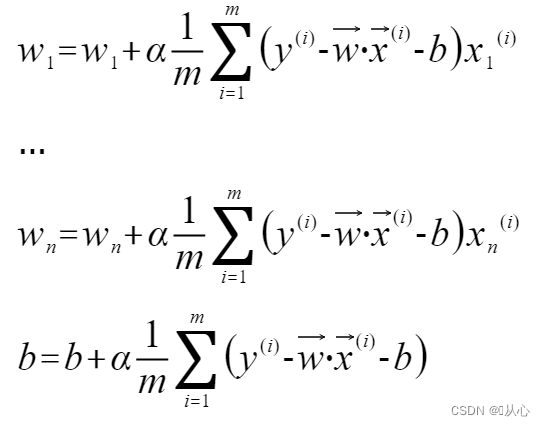


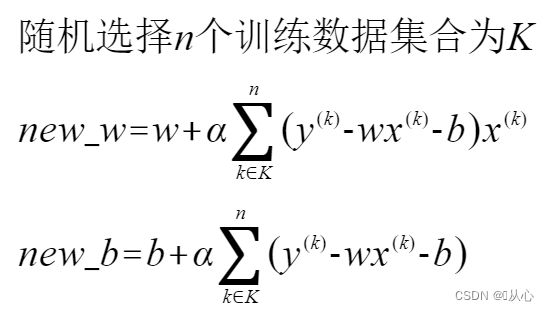

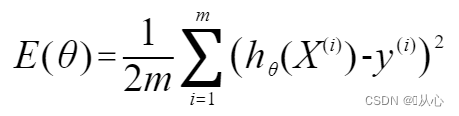

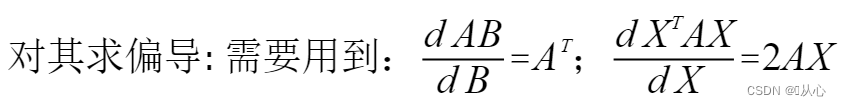

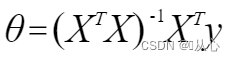













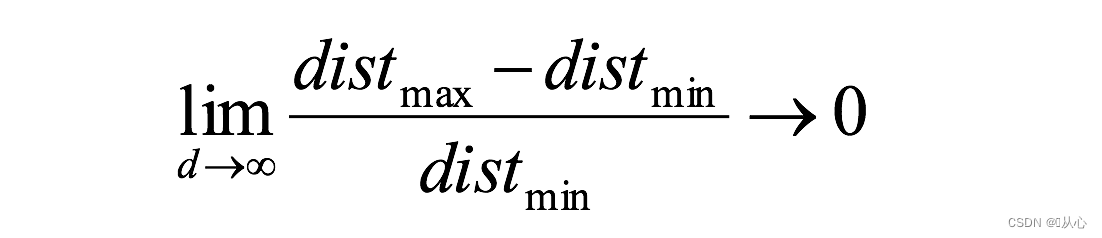






![[工业自动化-1]:PLC架构与工作原理](https://img-blog.csdnimg.cn/ce10a1471ed14382bc58364cf8bd5209.png)






还没有评论,来说两句吧...