更好的阅读体验

CF249D - Donkey and Stars

Description

给定 n n n 个点 ( x i , y i ) (x_i,y_i) (xi​,yi​) 和 a , b , c , d a,b,c,d a,b,c,d，求出最多有多少个点依次连接而成的折线上线段的斜率在 ( a b , c d ) (\frac{a}{b},\frac{c}{d}) (ba​,dc​)，其中第 1 1 1 条折线的起点必须在坐标原点且坐标原点不计入答案。

1 ≤ n ≤ 1 0 5 , 0 ≤ a , b , c , d ≤ 1 0 5 , 1 ≤ x i , y i ≤ 1 0 5 1\le n\le 10^5,0\le a,b,c,d\le 10^5,1\le x_i,y_i\le 10^5 1≤n≤105,0≤a,b,c,d≤105,1≤xi​,yi​≤105

Solution

不难想到通过 DP 来求解，暴力 DP 时间复杂度为 O ( n 2 ) O(n^2) O(n2)，必然是过不去的。所以，考虑对于点 i i i，能够与 i i i 连线的点 j j j 应满足哪些性质？

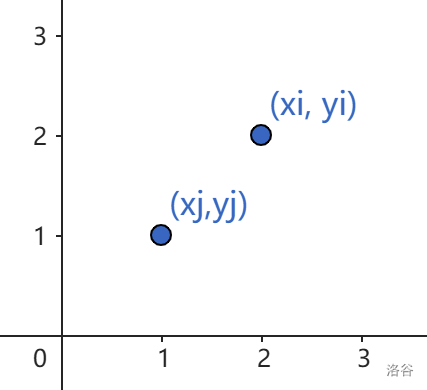
令 i i i 点位于 j j j 点的右上方，则有 a b < y i − y j x i − x j < c d \frac{a}{b}< \frac{y_i-y_j}{x_i-x_j}<\frac{c}{d} ba​

综上所述，可以做到 O ( n log ⁡ n ) O(n\log n) O(nlogn)。

Code

#include 
#define fi first
#define se second
#define int long long
using namespace std;
typedef pair PII;
typedef long long LL;
const int N = 1e5 + 10;
int n, a, b, c, d;
PII pnt[N];
int f[N];
std::vector dct;
struct fenwick {
	int tr[N];
	void add(int x, int d) { for (int i = x; i < N; i += (i & -i)) tr[i] = max(tr[i], d); }
	int sum(int x) {
		int res = 0;
		if (!x) return res;
		for (int i = x; i; i -= (i & -i)) res = max(res, tr[i]);
		return res;
	}
}cnt;
int find(int x) {
	return lower_bound(dct.begin(), dct.end(), x) - dct.begin() + 1;
}
signed main() {
	scanf("%lld\n%lld/%lld %lld/%lld", &n, &a, &b, &c, &d);
	for (int i = 1; i <= n; i ++)
		scanf("%lld%lld", &pnt[i].fi, &pnt[i].se), dct.push_back(d * pnt[i].se - c * pnt[i].fi);
	pnt[0] = {0, 0};
	sort(dct.begin(), dct.end());
	dct.erase(unique(dct.begin(), dct.end()), dct.end());
	sort(pnt, pnt + 1 + n, [&](PII tmp1, PII tmp2) {
		return tmp1.se * b - tmp1.fi * a < tmp2.se * b - tmp2.fi * a;
	});
	for (int i = n, j = n; i >= 0; i --) {
		while (j > i && pnt[j].se * b - pnt[j].fi * a != pnt[i].se * b - pnt[i].fi * a)
			cnt.add(find(pnt[j].se * d - pnt[j].fi * c), f[j]), j --;
		f[i] = cnt.sum(find(pnt[i].se * d - pnt[i].fi * c) - 1) + 1;
	}
	for (int i = 0; i <= n; i ++)
		if (pnt[i] == make_pair(0ll, 0ll)) {
			cout << f[i] - 1 << endl;
			return 0;
		}
	return 0;
 }