目录
- 一、MATLAB中传递函数的表示
- 二、rlocus函数绘制根轨迹
- 1.常规根轨迹仿真示例
- 2.参数根轨迹仿真示例
- 3.零度根轨迹仿真示例
- 三、图形化工具rltool介绍
一、MATLAB中传递函数的表示
在绘制系统的根轨迹之前,需要知道传递函数在matlab中如何表示。
在matlab中,通常用向量表示一个多项式。例如P=[1 2 3 ]表示 F(s)=s2+2s+3。而对于传递函数的表示,通常利用一个向量num表示其分子多项式,den表示分母多项式。例如表示 F ( s ) = 3 s 2 + s s 3 + 5 s + 8 F(s)=\frac{3s^2+s}{s^3+5s+8} F(s)=s3+5s+83s2+s的代码如下:
clear all; close all; num=[3 1 0]; den=[1 0 5 8]; sys=tf(num,den)
运行结果:
sys = 3 s^2 + s ------------- s^3 + 5 s + 8 Continuous-time transfer function.如果是两个多项式是相乘的形式,可以利用conv()函数。例如Fs=(s2+3s+1)(4s+1),则可以用den=conv([1 3 1],[4 1])计算出两个多项式相乘后的系数。
二、rlocus函数绘制根轨迹
MATLAB提供rlocus函数可以直接用于绘制系统的根轨迹。还能够允许用户交互式的选取根轨迹上的值。下表是rlocus函数的常见用法。
函数 使用说明 rlocus(G) 绘制开环传递函数为G的根轨迹 rlocus(G1,G2,…) 在同一张图上绘制多个系统的根轨迹 rlocus(G,k) 绘制系统的给定增益向量k的根轨迹 [r,k]=rlocus(G) 返回根轨迹参数,r为闭环特征根 r=rlocus(G,k) 返回系统的开环增益为k时的闭环特征根 下面分别演示常规根轨迹、参数根轨迹和零度根轨迹的绘制步骤。
1.常规根轨迹仿真示例
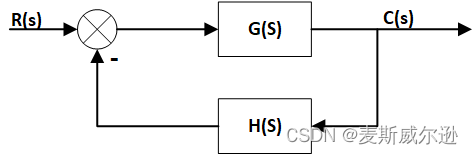
例: 某系统的结构如下图所示,绘制出其根轨迹。
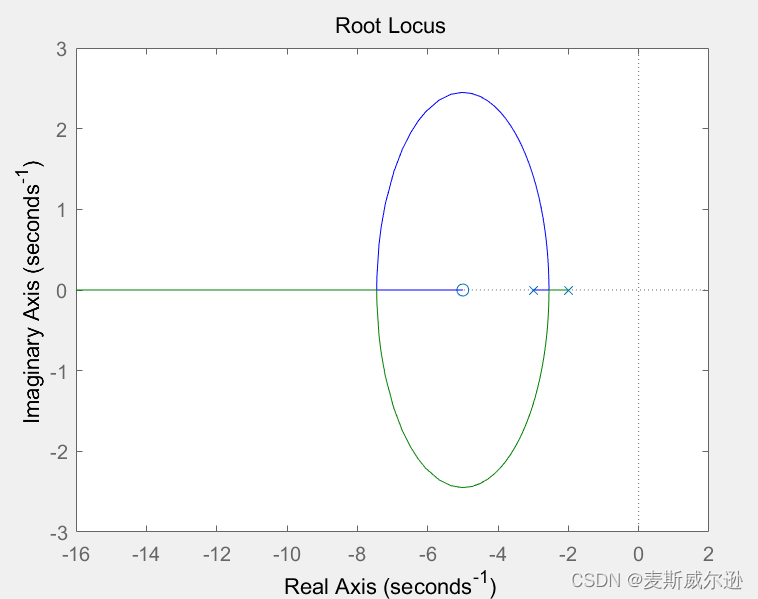
其中: G ( s ) H ( s ) = K ∗ ( s + 5 ) ( s + 2 ) ( s + 3 ) . G(s)H(s) = \frac{K^*(s+5)}{(s+2)(s+3)}. G(s)H(s)=(s+2)(s+3)K∗(s+5).
求解程序如下:
clear all; close all; num=[1 5];%num表示传递函数分子多项式系数向量 den=conv([1 2],[1 3]);%den表示传递函数分母多项式系数向量 sys=tf(num,den);%得到传递函数sys rlocus(sys)%绘制根轨迹,也可以用rlocus(num,den)直接绘制。
运行结果如下图:
2.参数根轨迹仿真示例
绘制参数根轨迹和绘制常规根轨迹的过程基本上相同。只需要在绘制参数根轨迹之前,引入“等效开环传递函数”,将绘制参数根轨迹的问题化为绘制K*变化时的根轨迹形式来处理。
例: 单位负反馈系统开环传递函数为 G ( s ) = k s ( s + 2 k ) . G(s) = \frac{k}{s(s+2k)}. G(s)=s(s+2k)k.
绘制出k=0→∞时的根轨迹。
解: 首先将上述传递函数转化为:
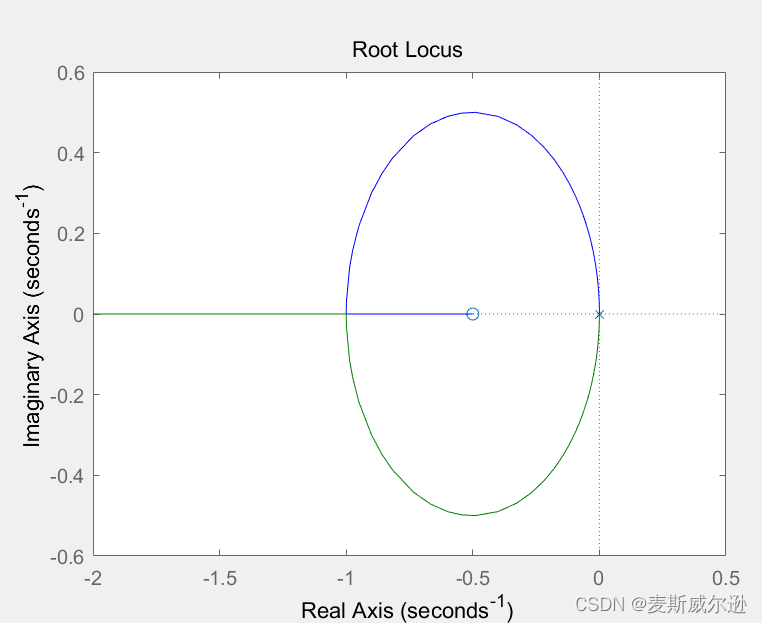
G ∗ ( s ) = k ( 2 s + 1 ) s 2 . G^*(s) = \frac{k(2s+1)}{s^2}. G∗(s)=s2k(2s+1).
然后就按照常规根轨迹的绘制步骤进行绘制,代码如下:
clear all; close all; num=[2 1]; den=[1 0 0]; rlocus(num,den);
运行结果如下:
3.零度根轨迹仿真示例
绘制零度根轨迹和绘制常规根轨迹的过程也基本上相同。唯一的差别是在绘制零度根轨迹时,需要在表示传递函数分子多项式的系数前添加一个负号,举个例子如下。
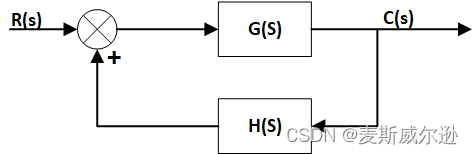
例: 某正反馈系统的结构图如下所示,
其中: G ( s ) H ( s ) = K ∗ s ( s + 5 ) ( s + 8 ) ( s 2 + 2 s + 2 ) . G(s)H(s) = \frac{K^*s(s+5)}{(s+8)(s^2+2s+2)}. G(s)H(s)=(s+8)(s2+2s+2)K∗s(s+5).
试绘制出根轨迹。
代码如下:
clear all; close all; num=[-1 -5 0]; den=conv([1 8],[1 2 2]); Gs=tf(num,den); rlocus(Gs)
运行结果如下:
三、图形化工具rltool介绍
MATLAB的rltool工具是一个图形化的工具,能够显示出系统的根轨迹以及系统的响应,同时也能够绘制系统的Bode图、奈奎斯特图和Nichols图等。rltool工具提供了一个非常直观的界面,帮助用户设计、分析和仿真控制系统,使得控制器的设计变得更加简单和高效。
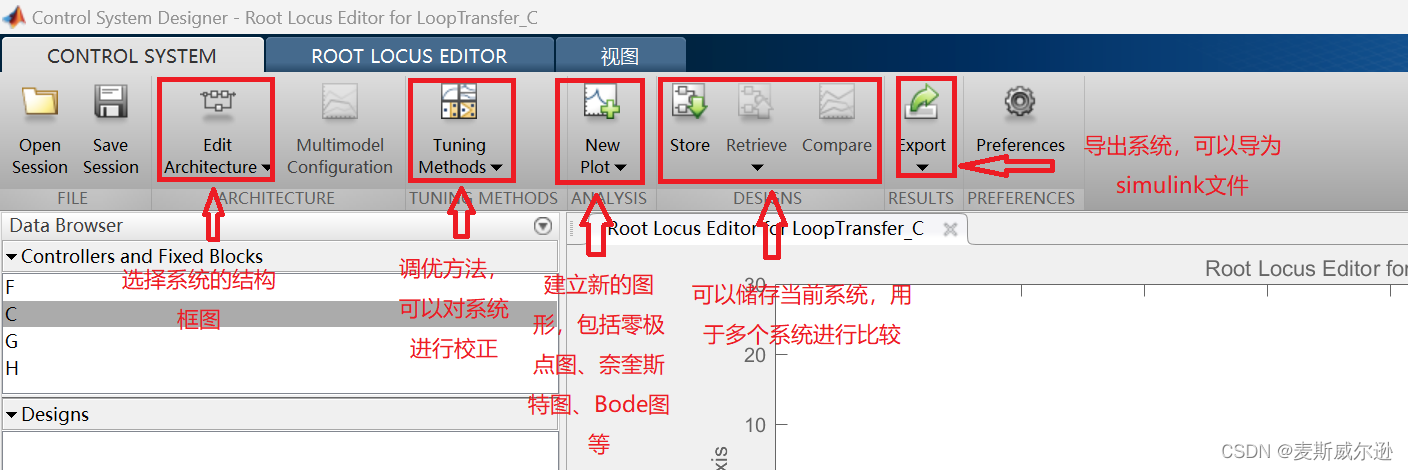
下图是rltool工具界面的介绍。
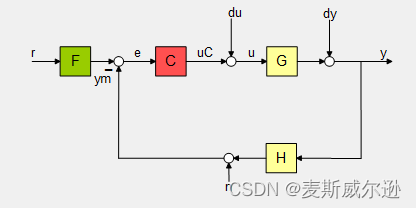
rltool工具默认的系统结构如下图所示,
其中G为被控对象,也就是输入rltool(sys)命令时传递函数sys,C为控制器(补偿器),在本文中C的值就是开环增益K的值。如果要改变系统的结构图,在菜单栏的第三项“Edit Architecture”中选择系统结构。
rltool常用命令如下表:
函数 说明 rltool 打开rltool工具 rltool(PLANT) 指定被控对象G的模型,PLANT是用TF、ZPK或SS创建的任何线性模型。 rltool(PLANT,COMP) 进一步指定控制器C的模型,COMP是用TF、ZPK或SS创建的任何线性模型。 rltool(PLANT,COMP,LocationFlag,FeedbackSign) LocationFlag指定控制器的位置,FeedbackSign决定反馈符号。LocationFlag=‘forward’时,控制器C在前向通道上;LocationFlag=‘feedback’时,控制器C在反馈回路上;FeedbackSign='-1’为负反馈;FeedbackSign=’1‘为正反馈。
通过以下的例子来简单介绍rltool工具的使用方法。
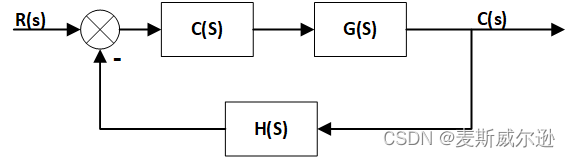
例: 某系统的方框图下图所示,
已知该系统为单位负反馈系统,被控对象为 G ( s ) = 1 s 3 + 20 s 2 + 100 s G(s)=\frac{1}{s^3+20s^2+100s} G(s)=s3+20s2+100s1,其中C(s)为比例控制器, C ( s ) = K C(s)=K C(s)=K,试绘制出K=0→∞时的系统根轨迹,另外讨论分别加入环节(s+4)和(s+2)对系统根轨迹的影响(C(s)=K(s+4)和C(s)=K(s+2)),并用阶跃响应验证结果。
解:
程序代码如下:
clear all; close all; num=[1]; den=[1 20 100 0]; Gs=tf(num,den);%建立被控对象传递函数 rltool(Gs)%打开rltool工具界面
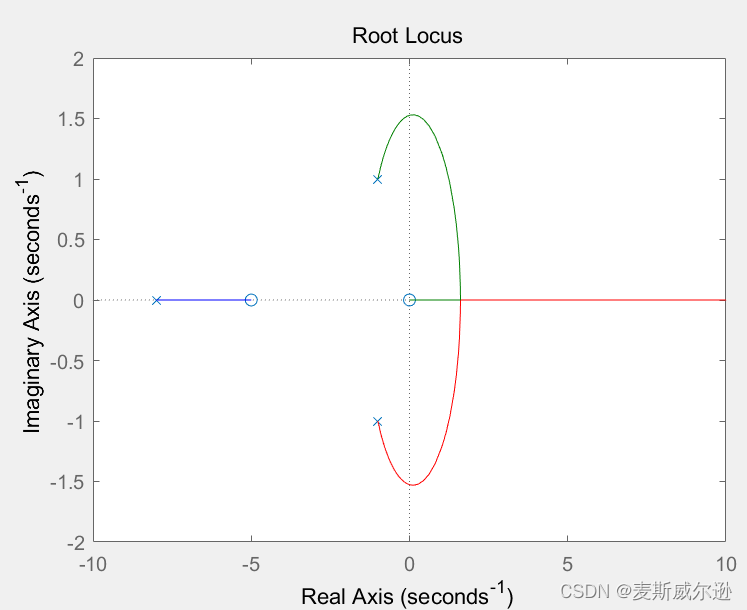
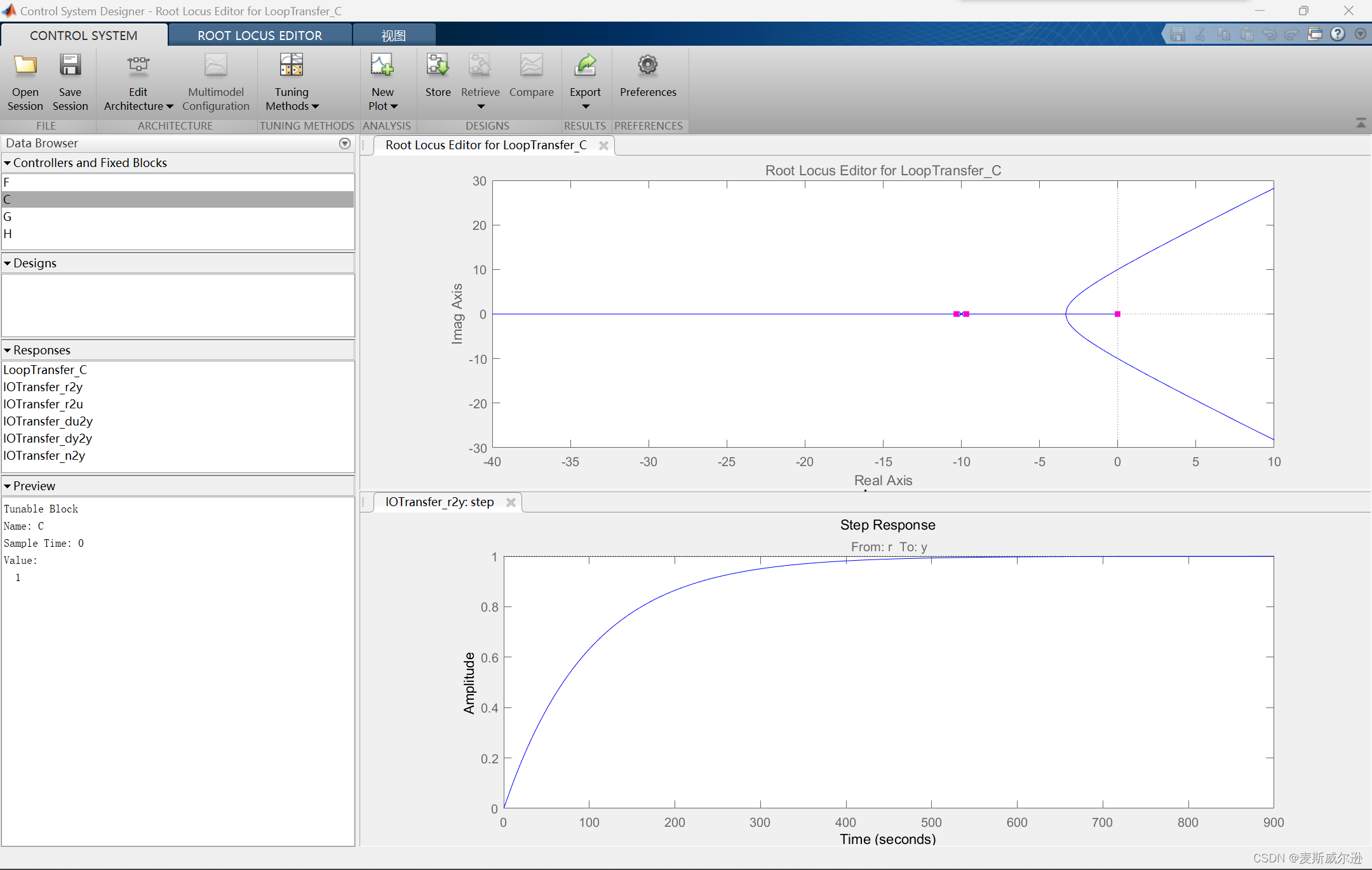
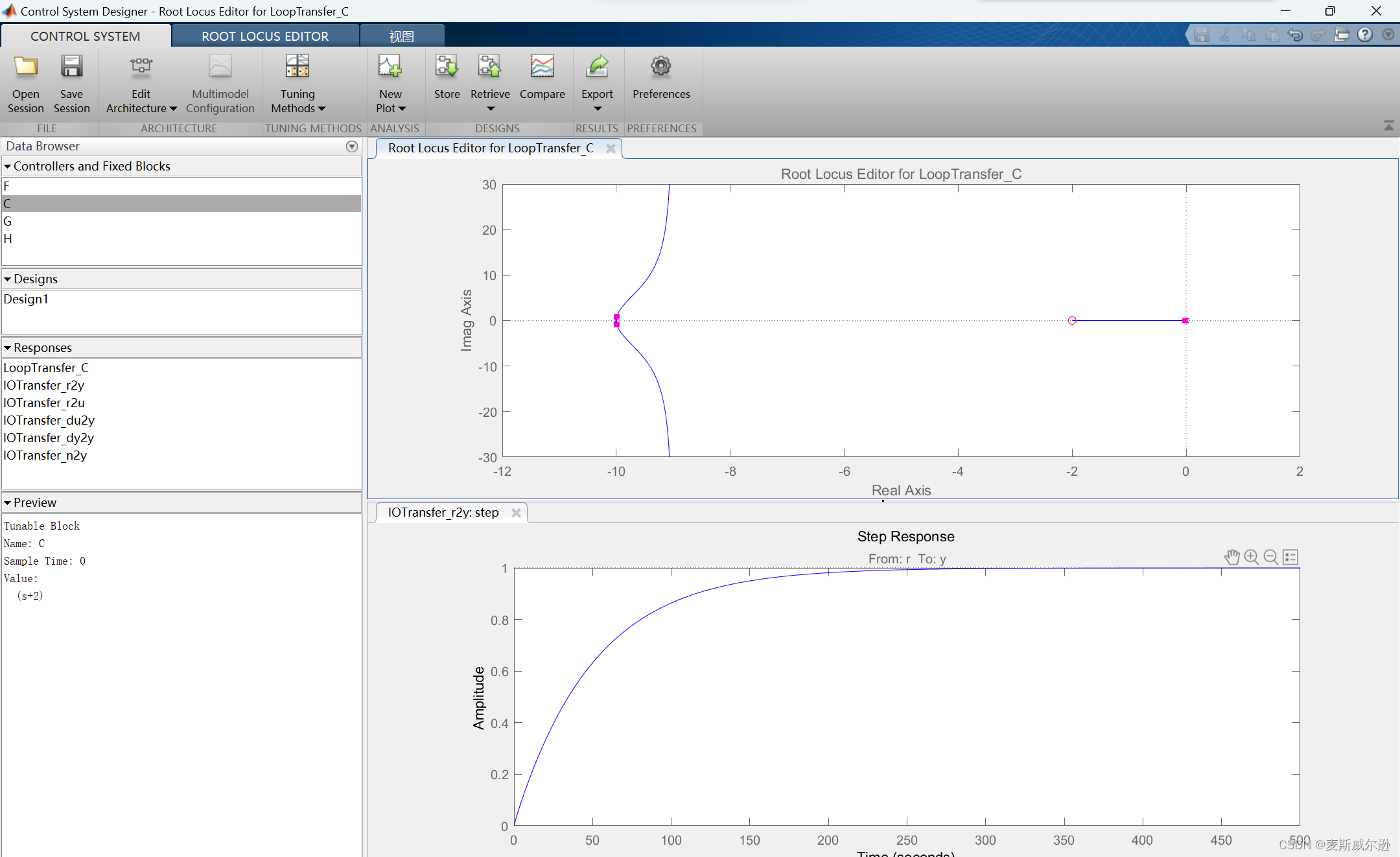
运行以上代码过后,进入到rltool工具的界面,如下图所示。其界面会显示出该系统的根轨迹图和K=1时系统的阶跃响应。根轨迹图中的红点表示当前系统的闭环特征根,可以拖动红点来改变当前系统的闭环特征根,拖动红点的同时系统的阶跃响应也会发生改变。而此时左边"Controllers or Fixed Blocks"状态栏中C的值就是当前系统的开环增益。
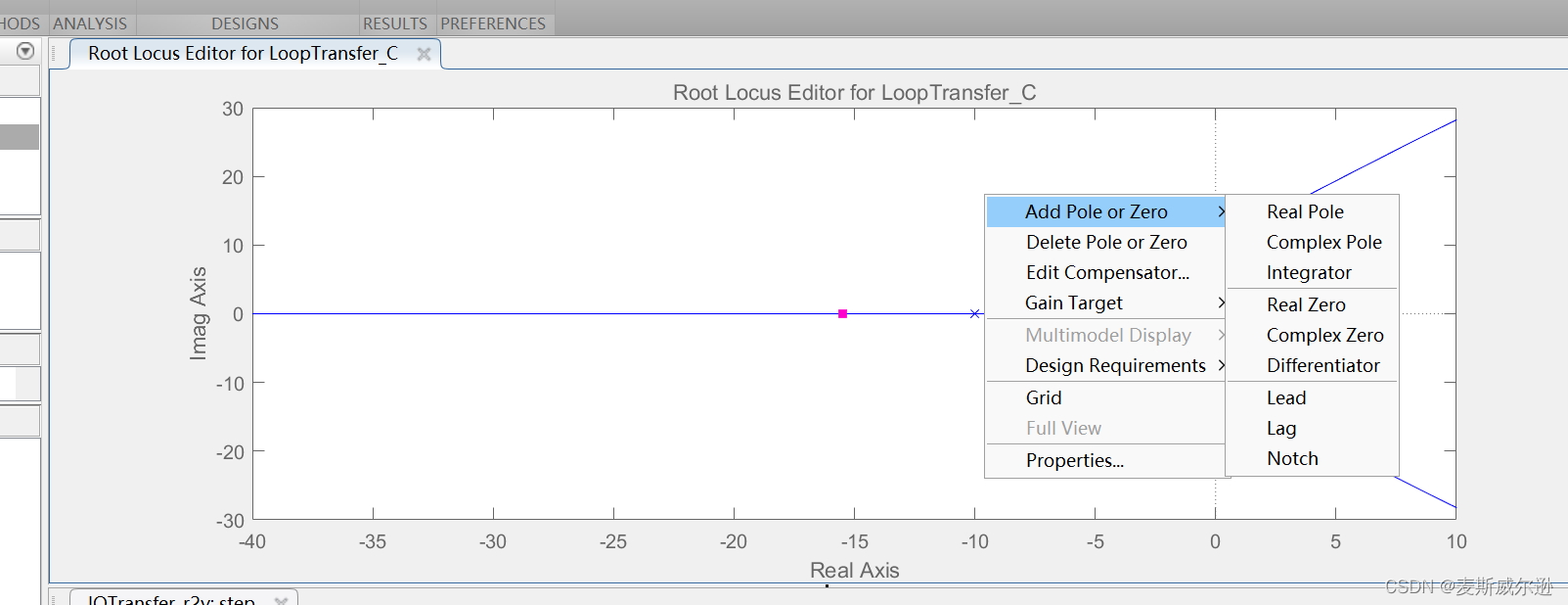
然后给系统添加一个环节(s+4),只需要在根轨迹图右击鼠标,选择添加零点极点"Add Pole or Zero"即可,如下如图所示,
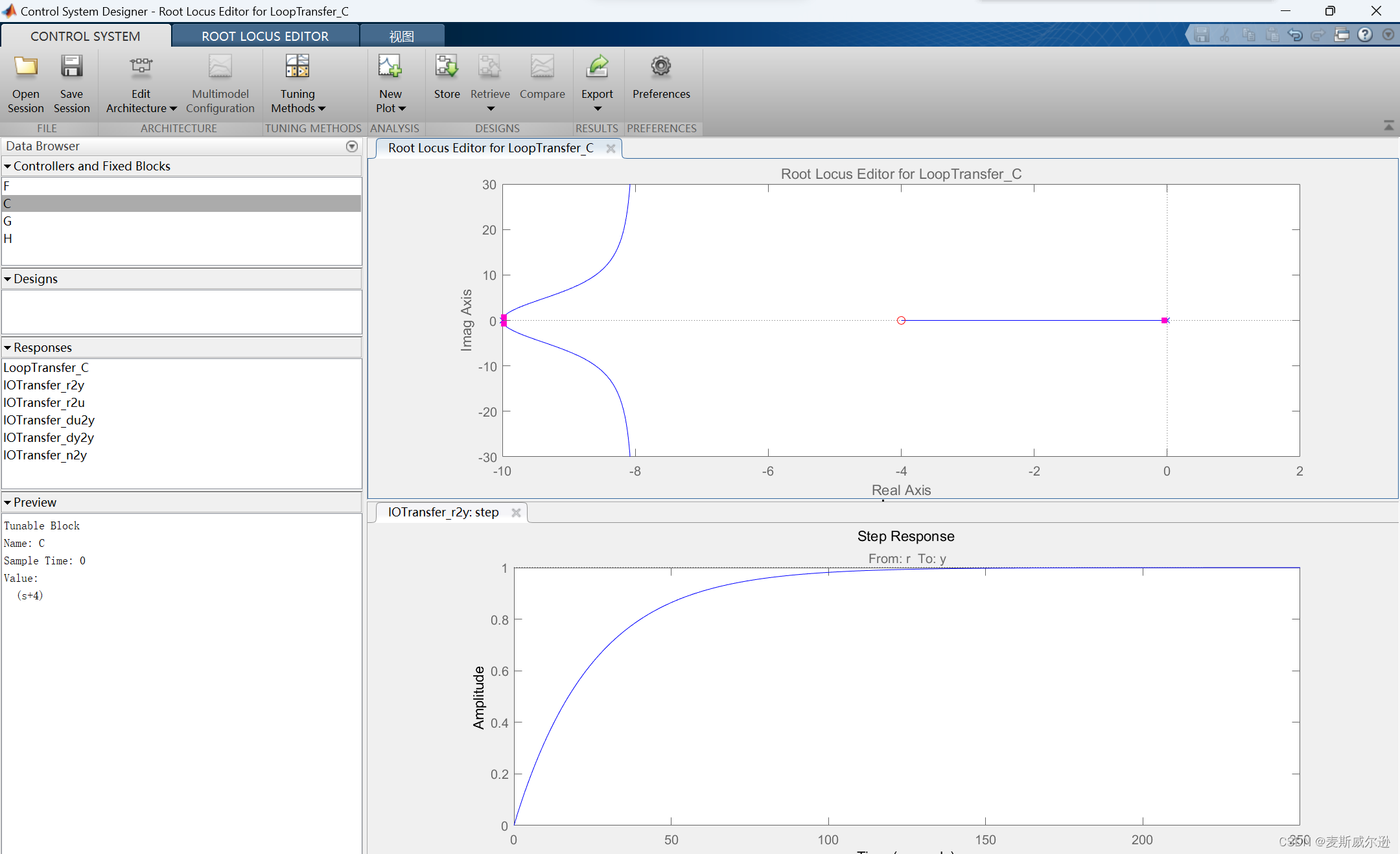
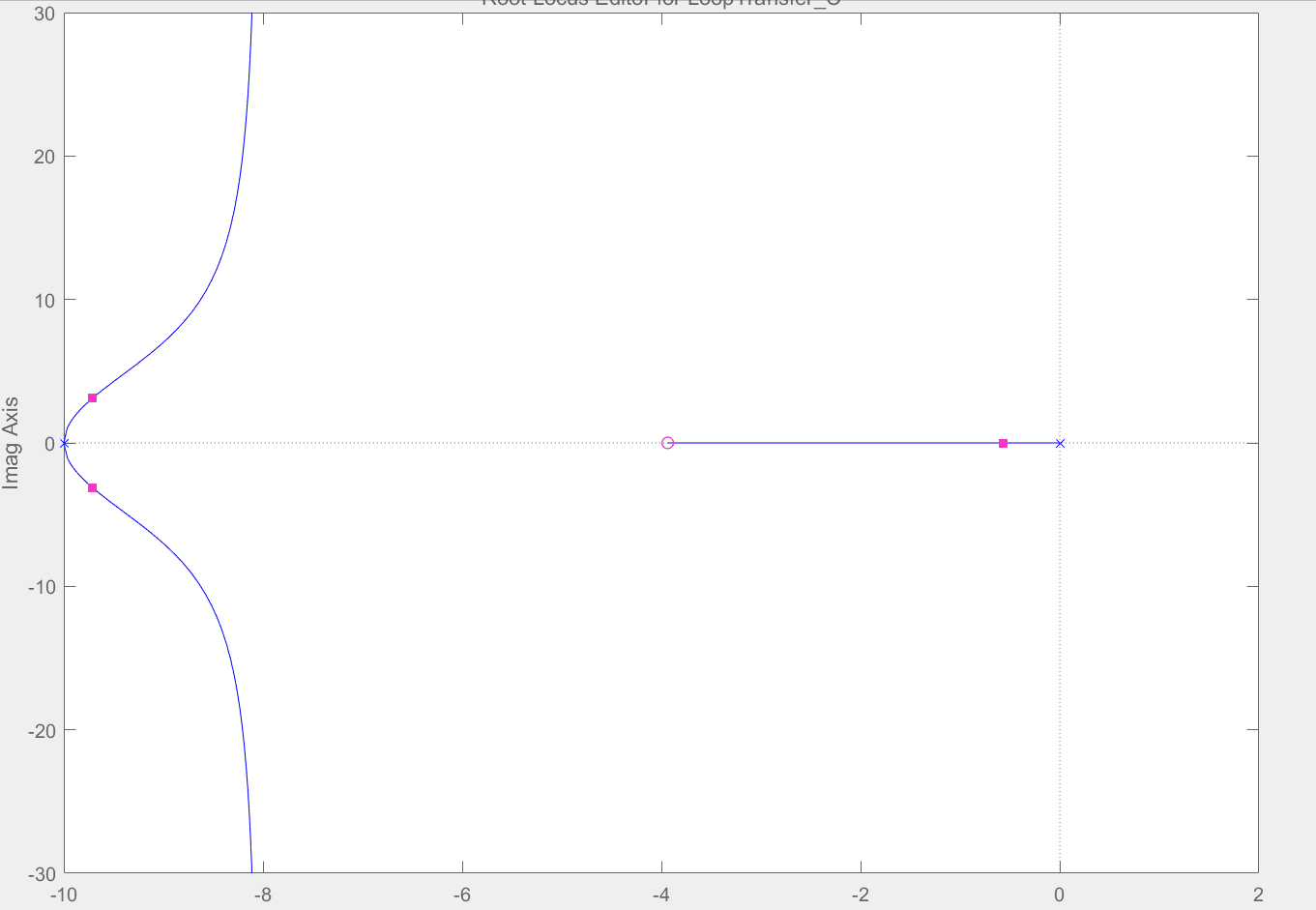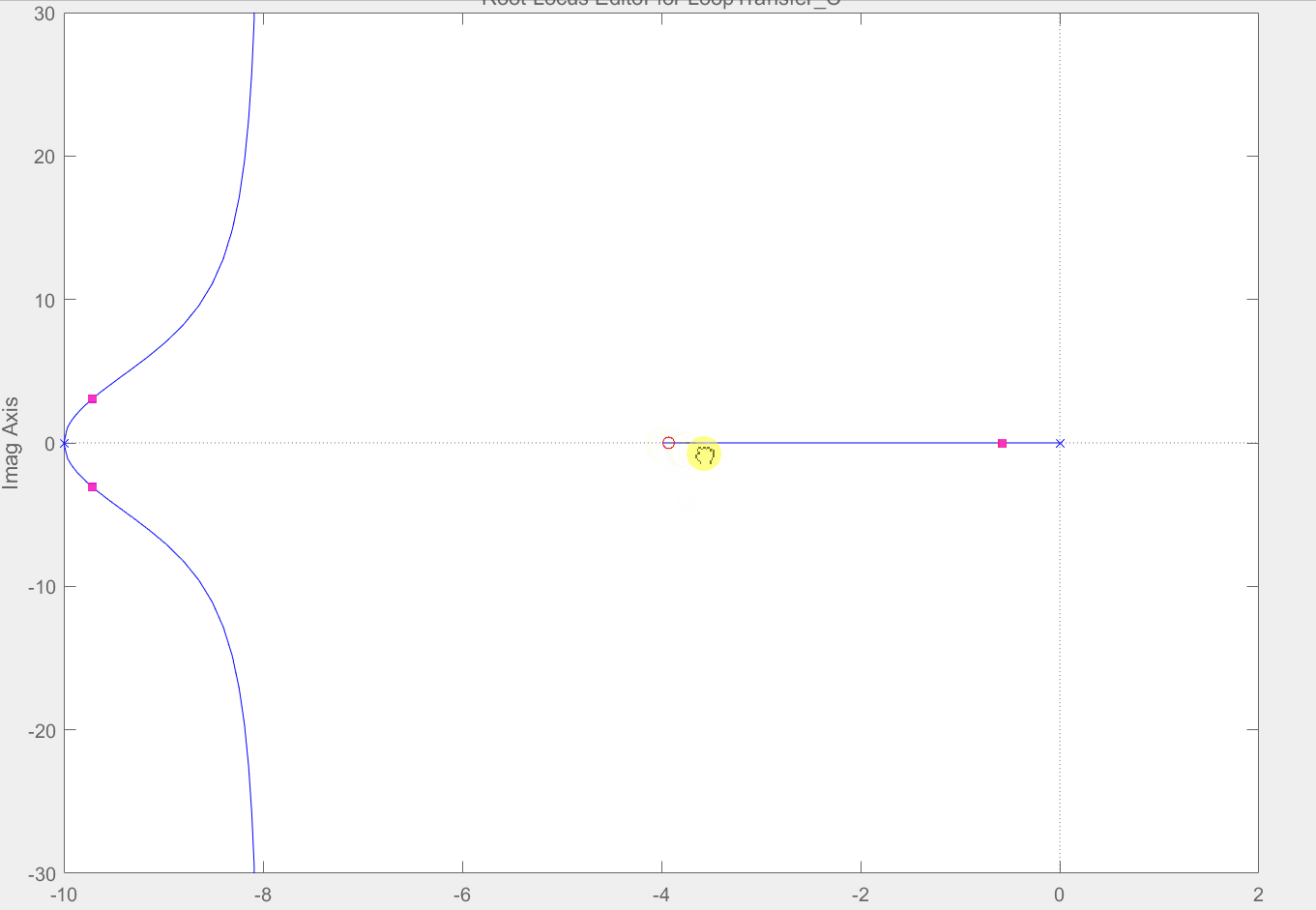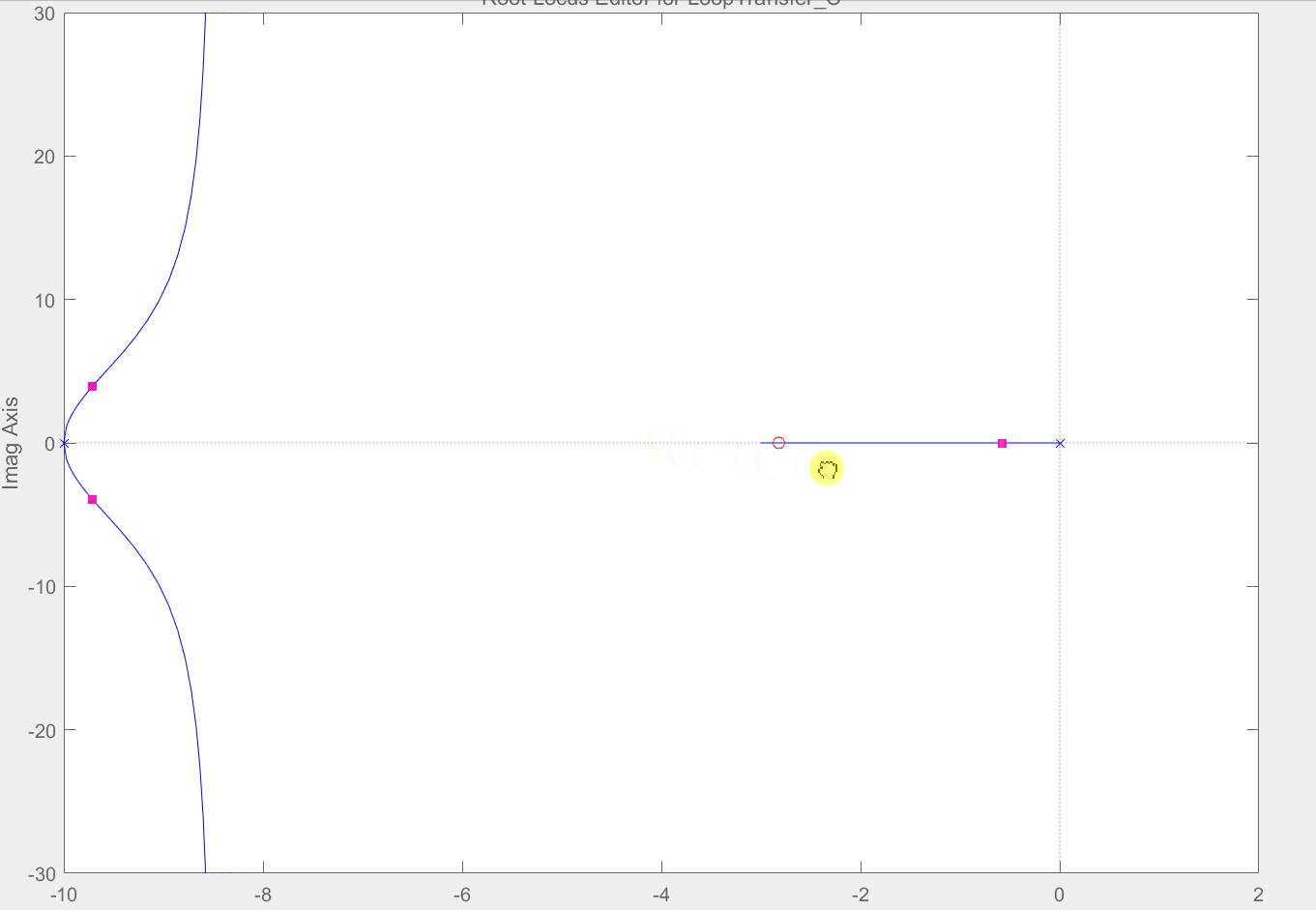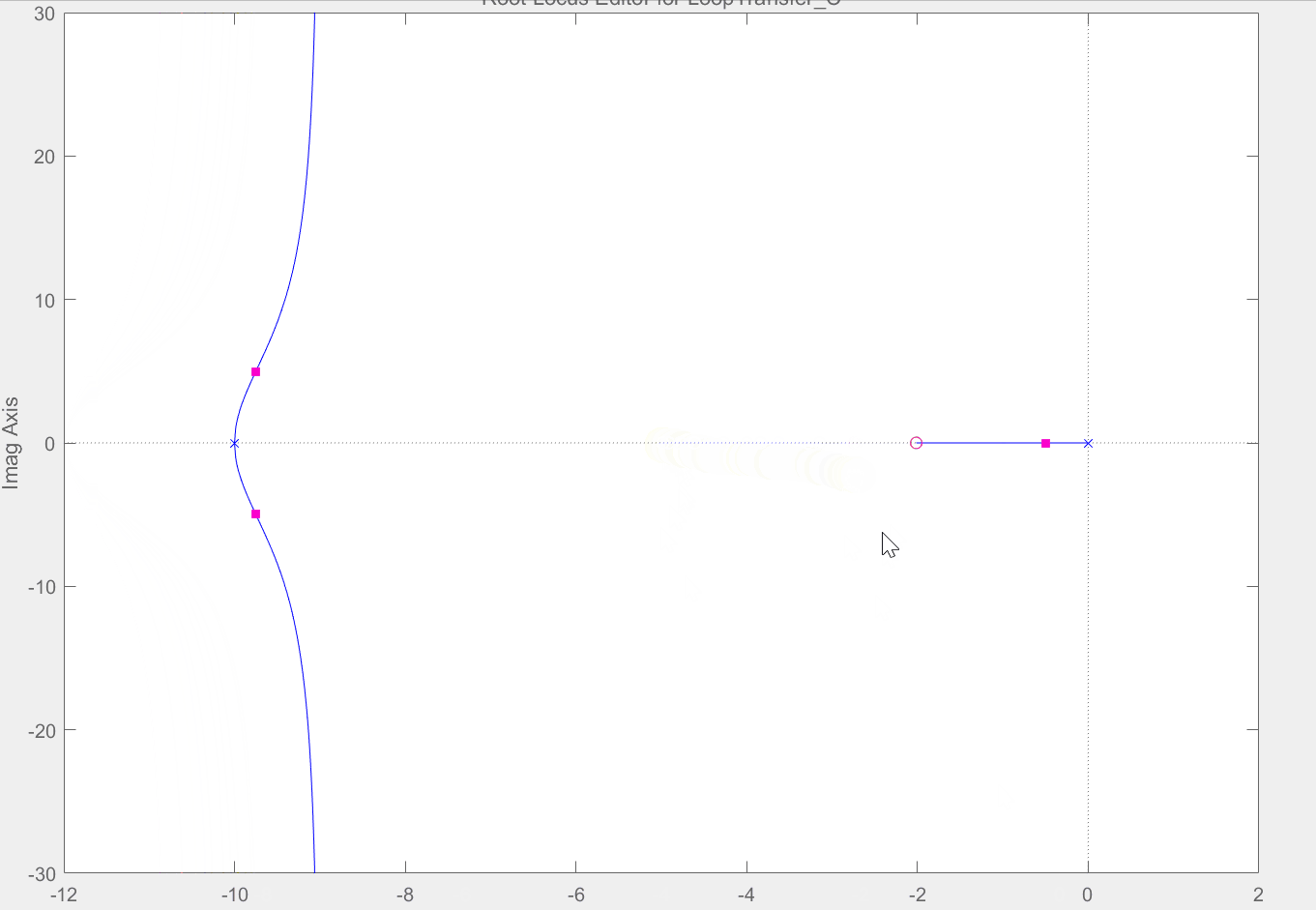
选择"Real Zero"添加实数零点,再在实数坐标上点击’-4‘的位置,添加完成后如下图所示,可以看到此时C的值为(s+4)。为了下一步能和添加环节(s+2)后对比系统的阶跃响应,先将该系统储存起来,点击菜单栏的"Store"选项储存为Design1。
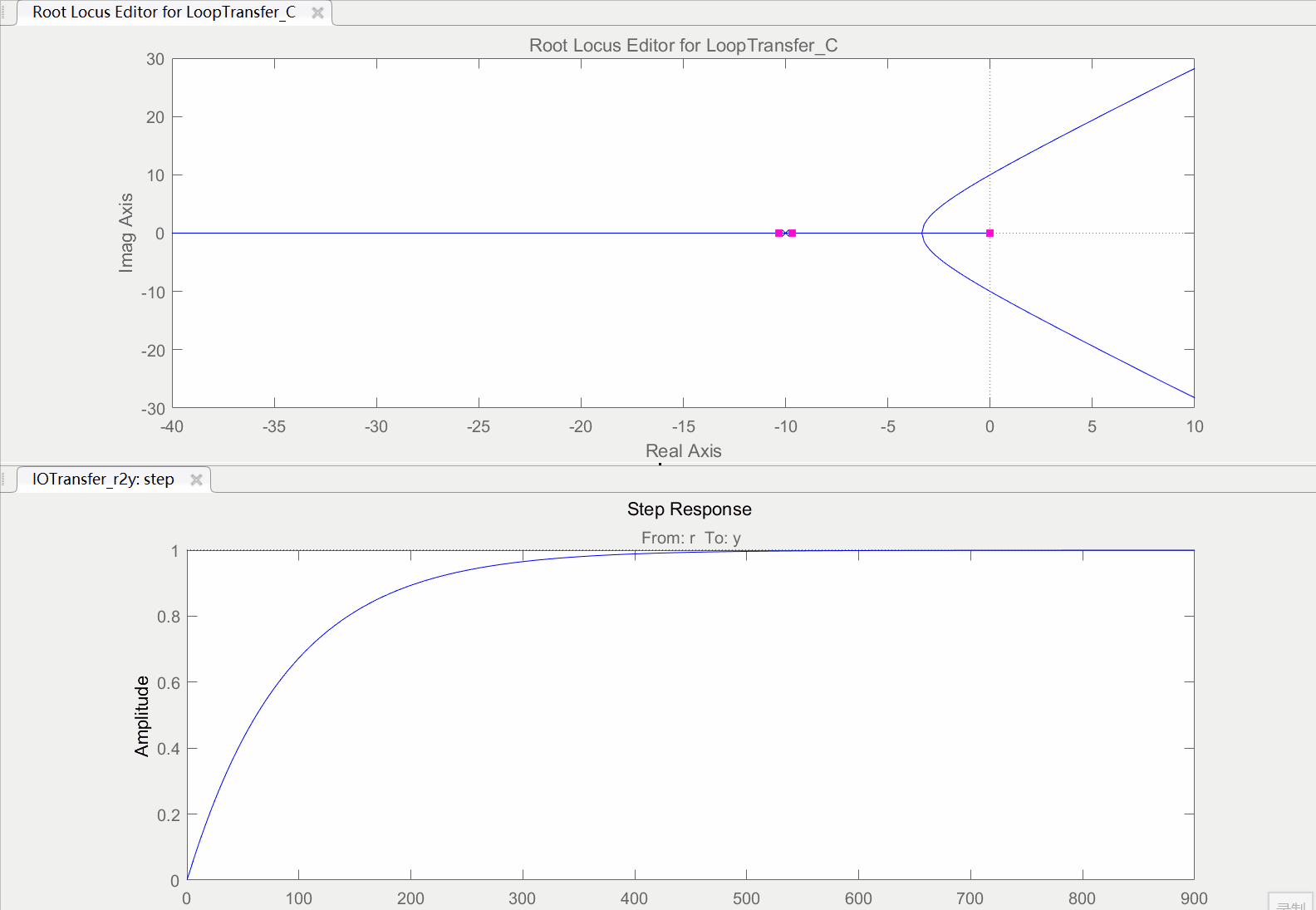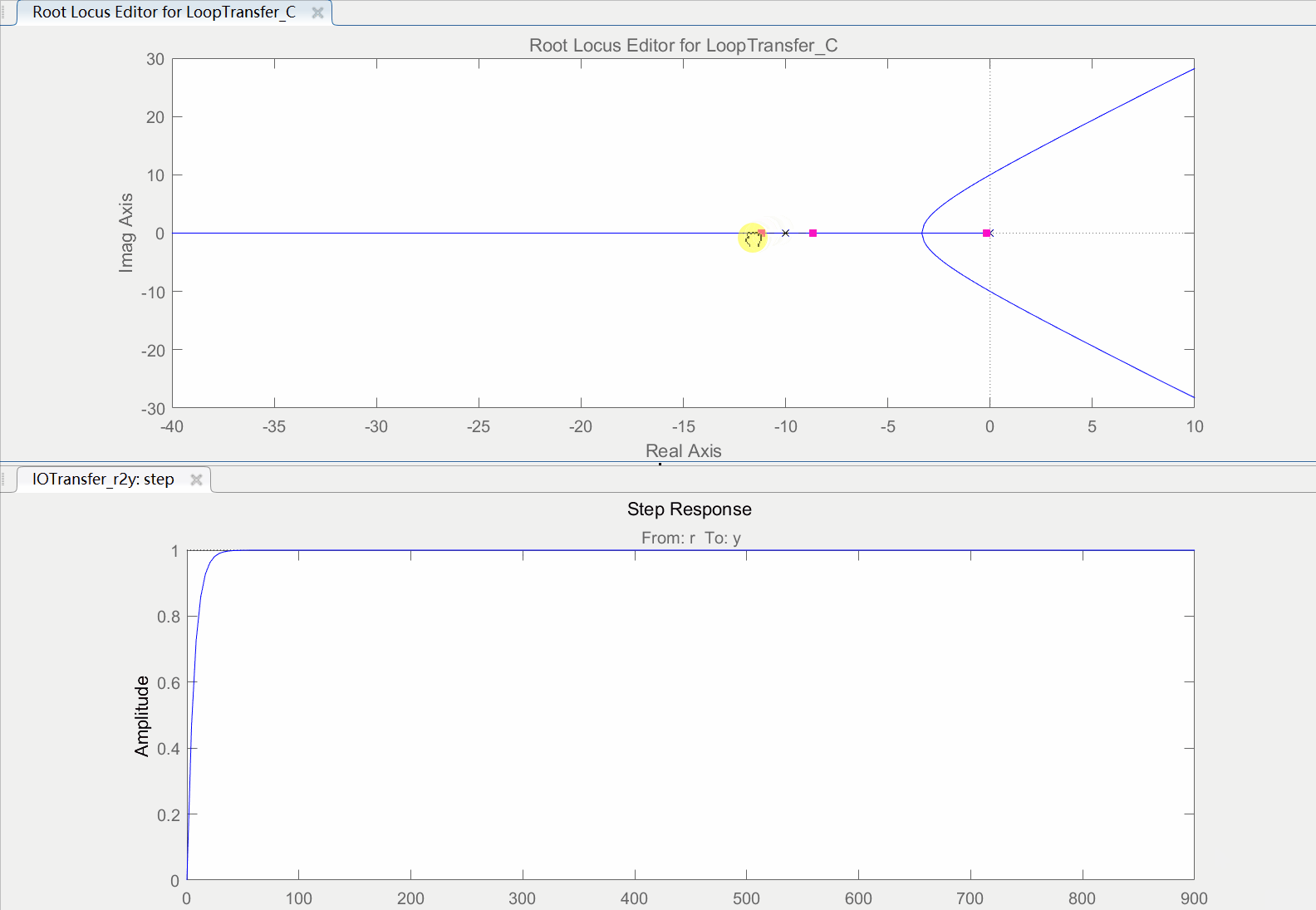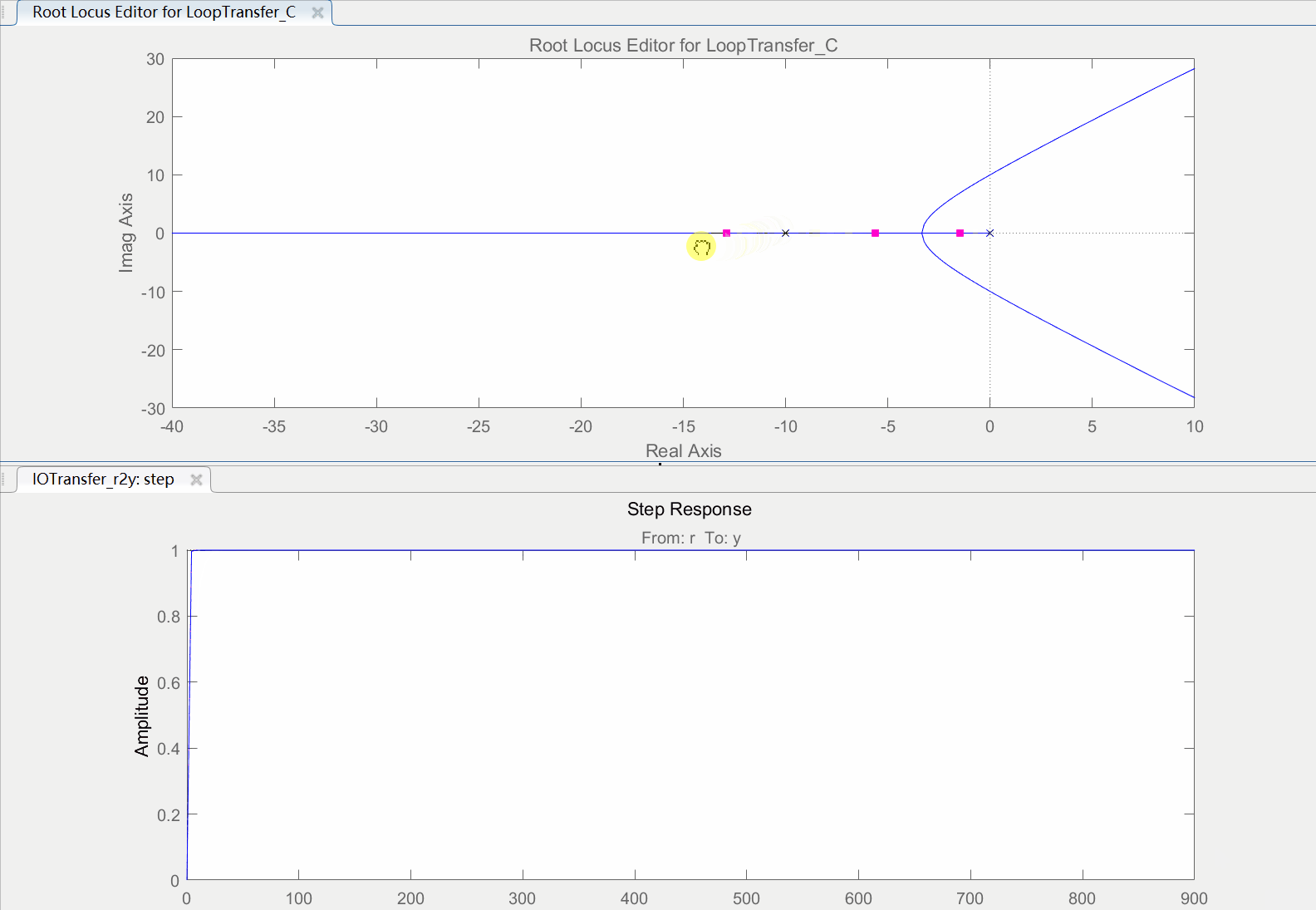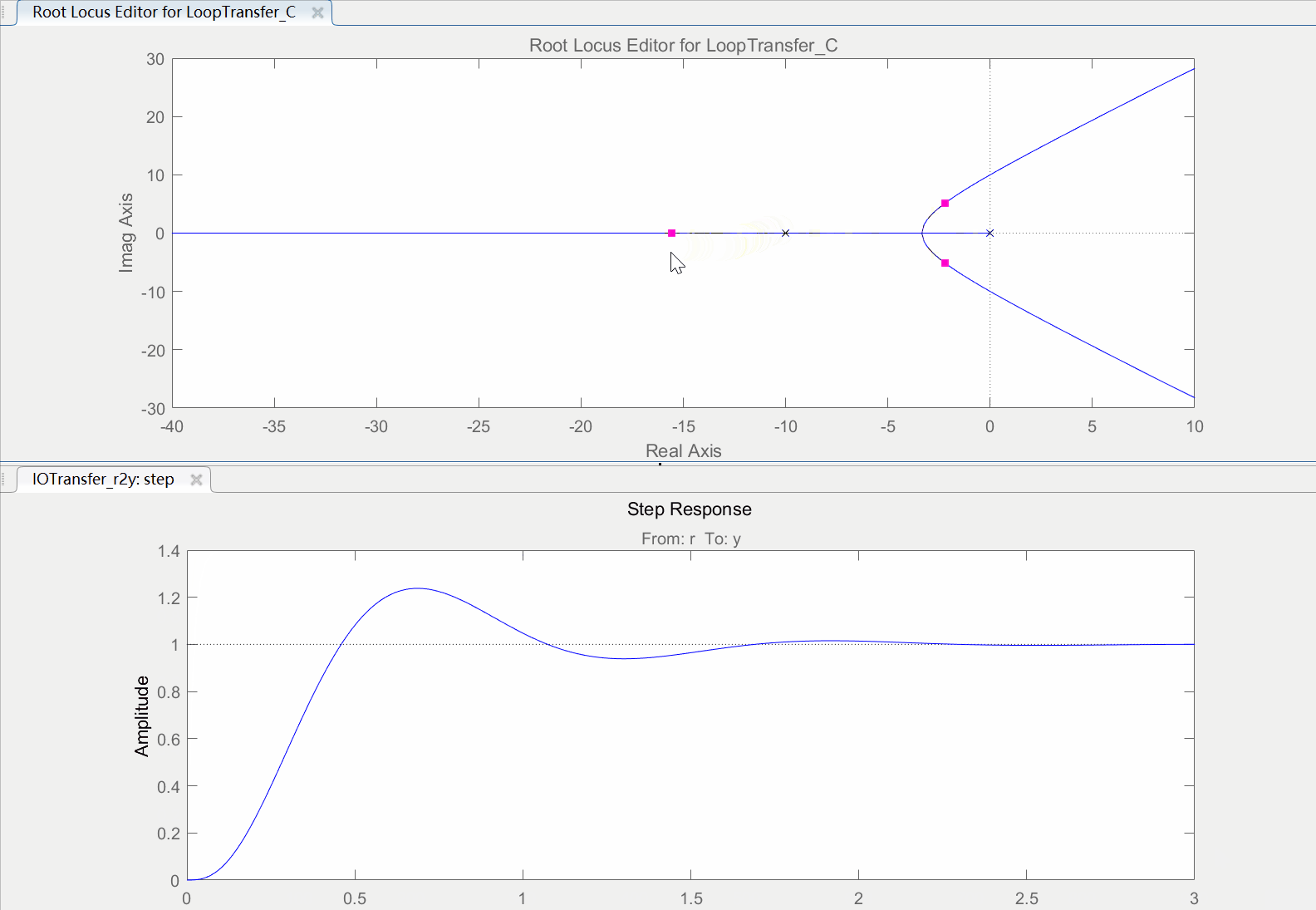
接下来添加环节(s+2),只需要将刚才的“-4”零点拖拽到“-2”处,添加过后的结果如下图所示,
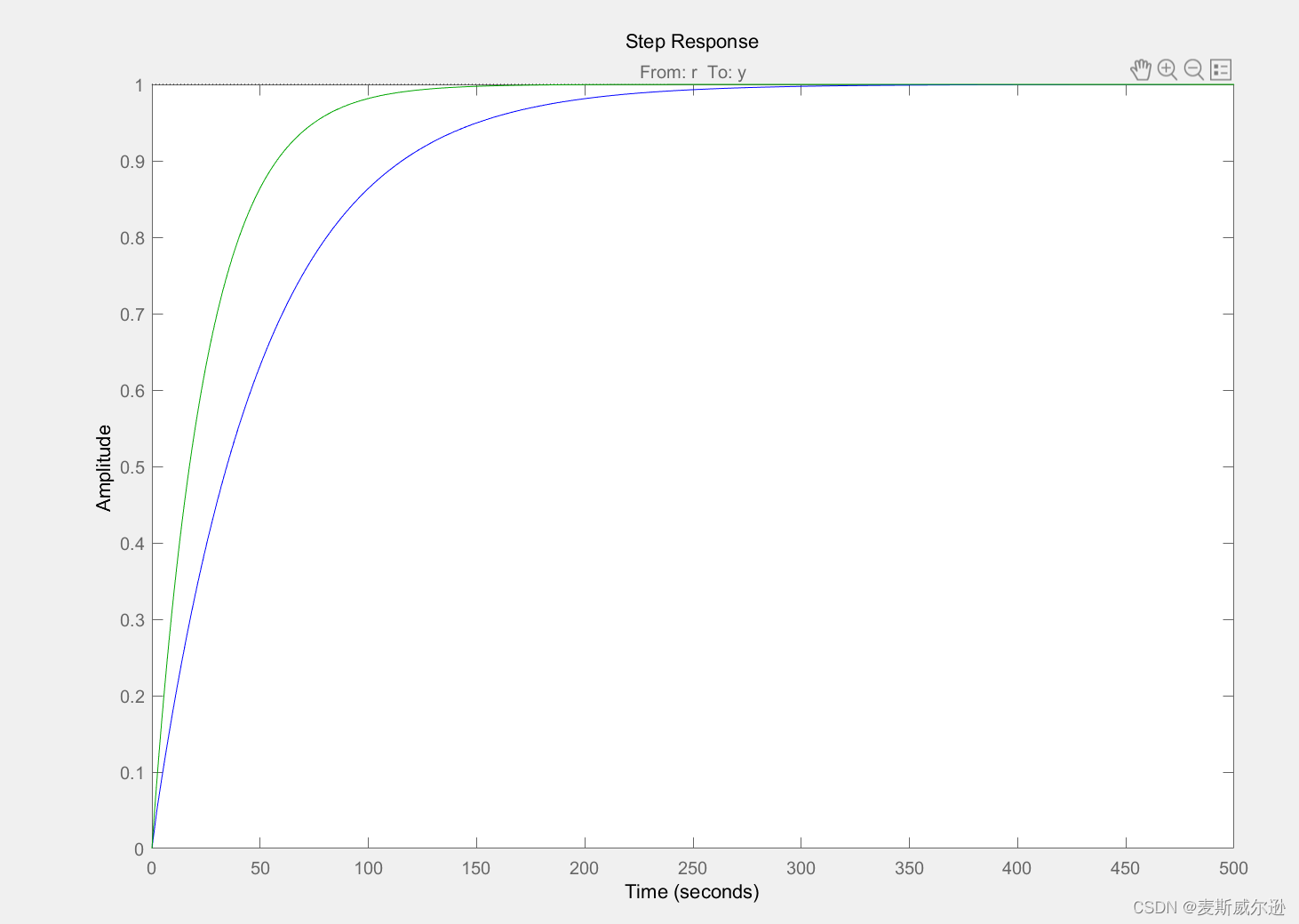
为了对比两个环节的阶跃响应,首先把两个系统的开环增益都设置为了1(也就是把控制图中C的值设置为1)然后再点击"Compare"选项选择Design1和当前系统进行对比,对比图如下,
其中,蓝色曲线为当前系统的阶跃响应(添加了环节(s+2)的系统),绿色曲线为Design1的系统阶跃响应(添加了环节(s+4)的系统)。
rltool的功能远不止画根轨迹,它也可以画Bode图、奈奎斯特图等等,能够对系统时域和频域分析起到很大的帮助,大家可以根据自己需要自行去探索


![[工业自动化-1]:PLC架构与工作原理](https://img-blog.csdnimg.cn/ce10a1471ed14382bc58364cf8bd5209.png)





还没有评论,来说两句吧...