文章目录

• 了解DFS
• 1.计算布尔二叉树的值
• • 思路
  • 代码展示
  • 2.求根节点到叶节点数字之和
  • • 思路
    • 代码展示
    • 3.二叉树剪枝
    • • 思路
      • 代码展示
      • 4.验证二叉搜索树
      • • 思路分析
        • 代码展示
        • 5.二叉搜索树中第k小元素
        • • 思路：
          • 代码展示
          • 6.二叉树的所有路径
          • • 思路分析
            • 代码展示
            • 总结

              了解DFS

              所谓DFS就是就是深度优先搜索，首先我们回到我们以前学习过的二叉树，对于二叉树我们讲过深度优先遍历，也就前序，后序，中序，这三种遍历方式，对于深度优先搜索，深度优先遍历是一个过程，在这个过程中我们加上搜索。

              在一颗二叉树上，对于遍历来说，我们会一条路走到黑，直到走到空的节点为止，才会返回上一个节点，走另一个分支，但是对于DFS（深度优先搜索）来说，我们的目的是、搜索当中的值，而不是一味地遍历。

              接下来我们通过几道题来深入理解这个算法

              1.计算布尔二叉树的值

              

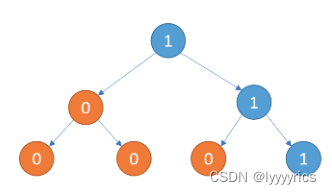
              首先我们来理解题意，题意很简单就是在一颗二叉树中只有0，1，2，3这几个值，他们分别代表的是false true || &&，我们来看看实际的一颗树：

              

              右边这颗二叉树就可以投影成左边这颗树的样子。

              接下来我们来分析一下这个道题应该怎么做：

              思路

              首先这道题说了这颗树是完整的二叉树，意思就是所有节点要么一个节点都没有，要么就是有两个节点。我们再来看这颗树的特征：非叶子节点肯定是2或者3，叶子节点肯定是1或者0，所以这里划分就出来了，我们对叶子节点和非叶子节点做不同的处理，如果是叶子节点就直接返回当前节点的值，如果不是叶子节点就判断一下该节点的值，如果是2就对左子树和右子树进行||操作，反之则进行&&操作即可。

              函数头

              函数头：bool dfs(root)

              函数体

              遇到叶子节点返回叶子节点的值，遇到非叶子节点，对左子树和右子树进行递归操作。

              递归出口

              就是返回叶子节点的值

              代码展示

              class Solution {
              public:
                  bool evaluateTree(TreeNode* root) {
                  	//只用判断一边就可以
                      if(root->right==nullptr)
                      {
                      	//叶子节点直接返回值
                          return root->val;
                      }
                      //得到左子树的结果
                      bool left=evaluateTree(root->left);
                      //得到右子树的结果
                      bool right=evaluateTree(root->right);
                      //判断一下当前节点的值是2还是3，进行&&操作还是||操作
                      return root->val==2?left||right:left&&right;
                  }
              };
              

              2.求根节点到叶节点数字之和

              

              题目解释：

              首先我们先给出一棵树

              

              对于这棵树并不是说所有节点的和就是把所有节点的值加起来，而是，我们先看第一个路径，4--9--5对于这个路径来说，这个路径下对应的和就是495，第二个路对应的是491，第三个路径对应的是40.

              从下面图应该可以看出：

              

              思路

              对于这道题，我们先来走一遍，当我们进入根节点4的时候，我们先递归左子树，我们肯定必须要知道前面的和是多少，因为我们要计算下一个节点的和，所以必须知道前面节点的和是多少，所以这里我们传递的参数就多了一个presum（前驱和）

              函数头

              函数头：int dfs(root,presum)

              因为这道题要求返回所有路径的和，所以有一个返回值就是int

              函数体

              这里我们来想一下函数体是什么？

              我们把presum传进行，当进入根节点的时候肯定不能带值，因为根节点的前驱和是0，所以这里我们传参的话，传presum进去先是0，进了函数之后我们先更新一下这个 presum，presum=presum*10+root->val,更新了presum之后，判断一下这个节点是否是叶子节点，如果是叶子节点直接返回presum，因为如果是叶子节点的话就说明这个路径的和已经求完了，只需要求下一个路径的和就可以了，这里我们用一个ret来存放一下左子树和右子树的和，如果左子树不为空，则返回将左子树的和加在ret上，如果右子树不为空，则再将右子树的和加在ret上，最后返回ret。

              代码展示

              class Solution {
              public:
                  int dfs(TreeNode*root,int presum)
                  {
                      //先将前驱和加上个
                      presum=presum*10+root->val;
                      //如果是末尾节点的话，直接返回前驱和
                      if(root->left==nullptr&&root->right==nullptr)
                      {
                          return presum;
                      }
                      int ret=0;
                      //如果左节点不为空的话直接ret叠加上左节点的dfs
                      if(root->left!=nullptr)
                      {
                          ret+=dfs(root->left,presum);
                      }
                      //如果右节点不为空的话只额吉ret叠加右节点的dfs
                      if(root->right!=nullptr)
                      {
                          ret+=dfs(root->right,presum);
                      }
                      //返回两边树的总和
                      return ret;
                  }
                  int sumNumbers(TreeNode* root) {
                      return dfs(root,0);//刚传递进去的时候前驱和是0
                  }
              };
              

              3.二叉树剪枝

              

              首先我们来看看下面一颗二叉树，注意这颗二叉树上只有1或者0.

              

              根据题目的意思，就是将只含有0的子树删除，对于上面这颗二叉树来说，只含有0的子树，首先我们看左子树，左子树全是零，直接删除，再看右子树，右子树的第一个节点是1，不满足，不能删除，右子树的左子树的节点，只有0，直接删除，右子树右子树只有1，不能删除，所以删除之后的二叉树就变成了下面的样子：

              

              思路

              对于这道题，我们要删除节点的话，肯定要知道左子树和右子树的信息，才能删除这个节点，由于这个特殊的性质，我们首先想到的则是后序遍历，因为只有后序遍历，才能将左子树和右子树的信息传递给节点，确定了该如何遍历之后，我们来讨论应该如何删除节点，首先我们肯定不能从非叶子节点开始删，因为我们根本不知道他的左子树和右子树的信息，所以应该从叶子节点开始删，所以这里删除的标志就是判断叶子节点的值是否为0，如果为0，则返回nullptr，证明将这个节点删除了，nullptr就是将删除的信息带给非叶子节点，如果叶子节点不是0，则返回当前节点，如果返回的是非空节点这个信息的话，就表示它的子树不是0，

              函数头

              函数头：dfs(root)

              函数体

              就是上面所讲的

              递归出口

              当遇到空节点的时候，直接返回空节点。

              代码展示

              class Solution {
              public:
                  TreeNode* pruneTree(TreeNode* root) {
                      //空节点直接返回
                      if(root==nullptr)
                      {
                          return nullptr;
                      }
                      //递归左子树
                      root->left=pruneTree(root->left);
                      //递归右子树
                      root->right=pruneTree(root->right);
                      //判断叶子节点的值
                      if(root->left==nullptr&&root->right==nullptr&&root->val==0)
                      {
                          //delete root防止内存泄露
                          return nullptr;
                      }
                      //如果是1，则不删除
                      else
                      {
                          return root;
                      }
                  }
              };
              

              4.验证二叉搜索树

              

              题目很简单，就是验证一棵树是否是二叉搜索树，如果是，则直接返回true，如果不是则返回false

              思路分析

              首先我们要知道一个二叉搜索树的一个很重要的性质，就是它的中序遍历是一个有序序列，这是一个这道题重要的突破口，我们只需要记录它中序遍历的前驱的节点，然后与当前节点进行比较即可，如果比当前节点大则当前情况来看的话是二叉搜索树，如果不满足的话，直接返回false，根本不需要进行判断了。注意，当返回结果的时候，我们要求左子树和右子树都满足还有根节点都满足二叉搜索树，才是二叉搜索树，否则不是二叉搜索树

              函数头

              函数头：dfs(root)

              函数体

              在定义函数体的时候，我们最好将prev(前驱）定义为全局变量，因为全局变量，随着地递归不会改变，我们只能手动改变

              递归出口

              当递归到空节点的时候，直接返回true，因为空节点就是二叉搜索树

              代码展示

              class Solution {
                  long prev=LONG_MIN;
              public:
                  bool isValidBST(TreeNode* root) {
                      if(root==nullptr)
                      {
                          return true;
                      }
                      bool left=isValidBST(root->left);
                      //左子树都不满足，则不用递归右子树了
                      //剪枝
                      if(left==false)
                      {
                          return false;
                      }
                      //用cur表示当前节点是否满足
                      bool cur=false;
                      //如果满足则进入将cur置为true
                      if(root->val>prev)
                          cur=true;
                          //不满足直接返回false
                      else
                          return false;
                          //更新prevv
                      prev=root->val;
                      //递归右子树
                      bool right=isValidBST(root->right);
                      //返回左子树和右子树和当前节点是否满足是否是二叉搜索树
                      return left&&right&&cur;
                  }
              };
              

              5.二叉搜索树中第k小元素

              

              对于这道题还是和上一道题类似。

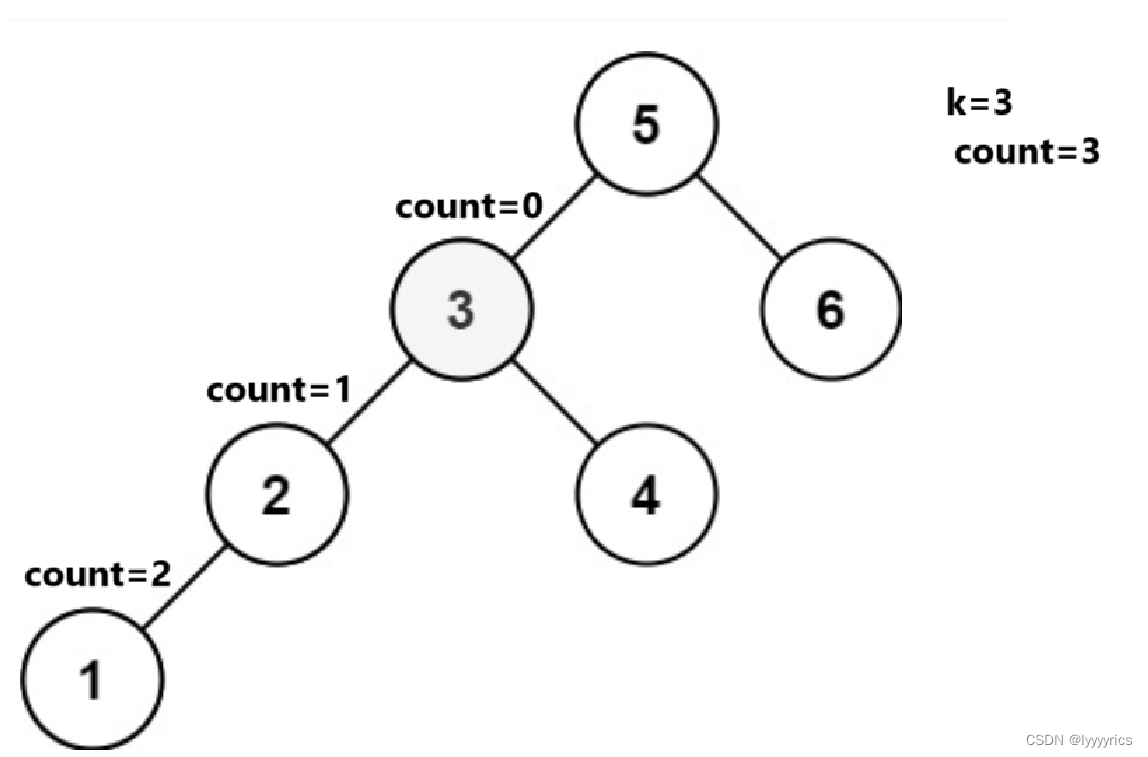
              思路：

              

              对于上面这个二叉搜索树，我们要求这个二叉搜索树的第k小的节点是不是应该用中序遍历，因为中序遍历是有序的，当我们中序遍历到叶子节点的时候，我们就可以开始数了，所以这里我们需要一个count来计数，计算这个是第几小，count我们最好选择全局变量，因为全局变量不会随着递归而改变，当我们中序遍历到叶子节点的时候，我们的count就应该–操作，每次–之后，我么都应该判断一下这个count是否已经==0了，如果等于0，我们用一个全局变量ret来接收一下这个值。

              

              到3的时候直接用全局变量接收这个值。

              代码展示

              class Solution {
                  int count;
                  int ret;
              public:
                  int kthSmallest(TreeNode* root, int k) {
                      count=k;
                      dfs(root);
                      return ret;
                  }
                  void dfs(TreeNode*root)
                  {
                      //count==0是剪枝
                      if(root==nullptr||count==0)return;
                      dfs(root->left);
                      count--;
                      if(count==0)
                      {
                          ret=root->val;
                      }
                      
                      dfs(root->right);
                  }
              };
              

              上面代码的递归出口的count==0，可不写，因为我们也可以继续递归，count为0只有一次，所以如果count等于0，我们可以直接不用递归了，直接返回。

              6.二叉树的所有路径

              

              这道题需要返回的是，一个路径的数组，类型是string类的

              思路分析

              这道题要返回string类的数组的话，为了不被递归影响到数组的值，所以我们最好还是创建一个全局变量数组，string的来记录这个每个路径，还需要一个局部变量，还需要一个string变量来记录当前路径。

              函数头

              函数头：dfs(root,path)

              传递一个局部变量的路径

              函数体

              注意函数体部分，我们分析一下，我们要求出所有路径，我们先看看下面的输入和输出样例。

              

              对于这个输出样例，我们可以看到这个string不仅需要路径的值还需要一个->将其串联起来，所以这里我们就分为了两种情况，一种是非叶子节点，一种是叶子节点，对于非叶子节点，我们不仅需要向string变量中加入当前值的字符，还需要向里加入两个符号“->”，但是对于叶子节点来说，我们只需要向里添加当前节点对应值的字符就可以了，注意：添加完之后，我们将string类的变量丢进string类的数组中，注意：这里我们不创建全局变量string的原因是因为当我们返回到上一节点的时候，因为全局变量不会改变，所以我们需要手动删除当前路径下的不需要的所有节点，才能进入下一个分支，就拿上面的图为例子，当我们要进入右子树的时候，我们必须将左子树中的2和3删完之后，只留下1才能进入右子树分支，但是对于局部变量，则不一样，注意：这里我们创建局部变量的时候，传参也要传拷贝构造，而不是引用，传引用的话和创建全局变量没有任何区别，传递拷贝构造的话，每次返回上一个分支都是一个新的string，不会存在什么删除不需要的情况。

              代码展示

              class Solution {
                  //全局若string数组，用来存储字符串
                  vector  ret;
              public:
                  vector binaryTreePaths(TreeNode* root)
                  {
                      //创建path记录路径
                      string path;
                      dfs(root,path);
                      //返回字符数组
                      return ret;
                  }
                  void dfs(TreeNode*root,string path)
                  {
                      //叶子节点的处理方式
                      if(root->left==nullptr&&root->right==nullptr)
                      {
                          path+=to_string(root->val);
                          ret.push_back(path);
                          return;
                      }
                      //非叶子节点的处理方式
                      path+=to_string(root->val)+"->";
                      //左子树不为空才递归，为空直接剪枝
                      if(root->left)dfs(root->left,path);
                      //右子树也一样
                      if(root->right)dfs(root->right,path);
                  }
              };
              

              总结

              通过本文的探讨，我们了解了深度优先搜索（DFS）在解决二叉树问题中的强大功能和广泛应用。DFS 通过其递归和迭代两种实现方式，为我们提供了处理二叉树的不同策略，使得问题的求解变得更加灵活。无论是前序遍历、中序遍历还是后序遍历，DFS 都能够有效地遍历二叉树的每一个节点，从而帮助我们解决各种实际问题，如路径求和、树的对称性检查以及节点间距离计算等。

              希望通过本文的介绍，大家对 DFS 在二叉树问题中的应用有了更深入的理解，并能够在实际编程中灵活运用这些技巧来解决复杂的树结构问题。感谢阅读，期待在你们的代码中见到这些算法的身影！如果有任何疑问或进一步的讨论，欢迎在评论区留言，我们一起交流学习。