数字信号处理翻转课堂笔记17——窗函数法设计FIR滤波器及matlab实现

码农世界 2024-06-08 后端 107 次浏览 0个评论

数字信号处理翻转课堂笔记17

The Flipped Classroom17 of DSP

对应教材：《数字信号处理（第五版）》西安电子科技大学出版社，丁玉美、高西全著

一、要点

（1）窗函数法设计FIR线性相位滤波器的原理；

（2）加窗效应：加窗对滤波器特性的影响（难点）；

（3）典型窗函数及其主要特性和参数（重点）；

（4）窗函数法设计FIR滤波器的步骤（重点）；

（5）窗函数法设计FIR滤波器的MATLAB函数及其应用。

二、问题与解答

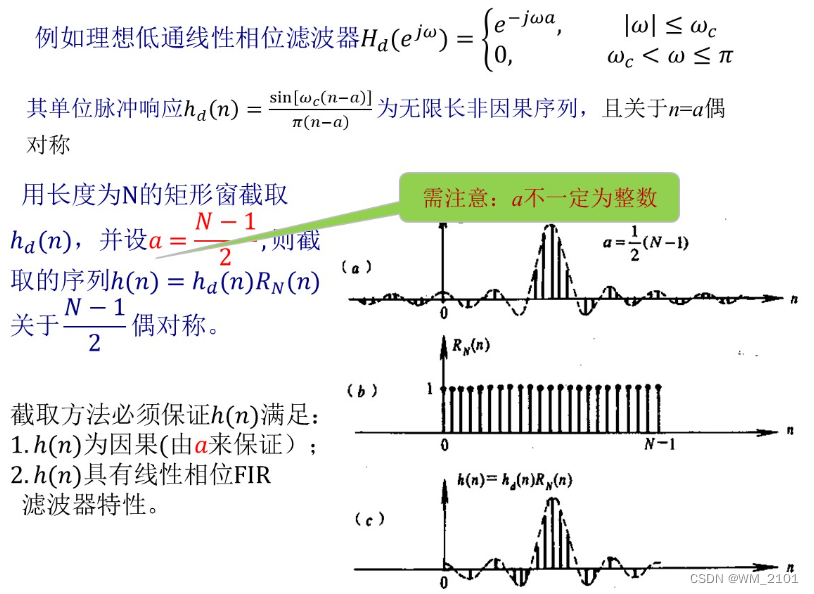
（1）简述窗函数法设计线性相位FIR滤波器的基本原理。在利用窗函数对理想滤波器单位响应进行截取时，如何同时保证所得FIR滤波器的因果性和线性相位特性？

（2）以矩形窗为例，参考教材图7.2.3，分析加窗效应的原理和结果。主瓣宽度、吉布斯效应的影响

（3）基于MATLAB，画出长度N分别为8、16、32的矩形窗函数的幅度谱，并画出基于矩形窗所设计的相应长度线性相位FIR低通滤波器的幅频响应。根据结果，总结分析滤波器长度N对阻带衰减、过渡带宽度的影响。

（4）自行设定一个固定的滤波器长度N，基于Matlab分别用不同的窗函数设计FIR线性相位高通滤波器（利用fir1函数），画出所设计滤波器的单位响应h(n)和幅频特性。根据所得结果，结合教材表7.2.2，总结各种窗函数的特性和参数。与教材给出的各种窗函数所设计的低通滤波器的单位响应进行比较，比较高通和低通FIR线性相位滤波器时域响应的不同特点。

（5）举例说明窗函数法设计FIR线性相位滤波器的步骤：自行给定滤波器类型和技术指标，利用窗函数法设计FIR线性相位滤波器，按照设计步骤手算（不用MATLAB编程）。

（6）设模拟信号x(t)=cos(800πt)+ cos(1000πt)+ cos(1600πt)，用2000Hz的采样频率对其数字化，得到相应的序列x(n)。分别设计IIR滤波器和FIR滤波器（窗函数法），对x(n)进行滤波，要求滤除其中的cos(1000πt)分量（衰减到原幅度的1%以下），且保留的两个频率分量幅度变化不超过1%。a) 请根据以上要求，确定数字滤波器的类型和技术指标参数，完成滤波器设计，并画出所设计IIR、FIR数字滤波器的幅频特性和相频特性、x(n)经过两种滤波器滤波前后的时域信号及其幅度频谱，比较其结果的异同并分析其原因。b) 设x1(t)由所保留的2个分量构成（x(t)=cos(800πt) + cos(1600πt)），y(n)是IIR滤波后的输出，yf(n)是FIR滤波后的输出，利用实验一的方法，对y(n)和yf(n)进行时域恢复，恢复结果分别为y(t)和yf(t)，分别画出x1(t)、y(t)和yf(t)，比较分析其异同，总结线性相位滤波器的优点。

1、窗函数的基本概念

简述窗函数法设计线性相位FIR滤波器的基本原理。在利用窗函数对理想滤波器单位响应进行截取时，如何同时保证所得FIR滤波器的因果性和线性相位特性？

保证因果性：因为a的存在使函数发生延迟而不是超前，所以保证了因果性。

保证线性相位特性：因为a是常数，所以a的存在使不同频率分量都具有相同的延时，满足了线性相位特性。

2、加窗效应

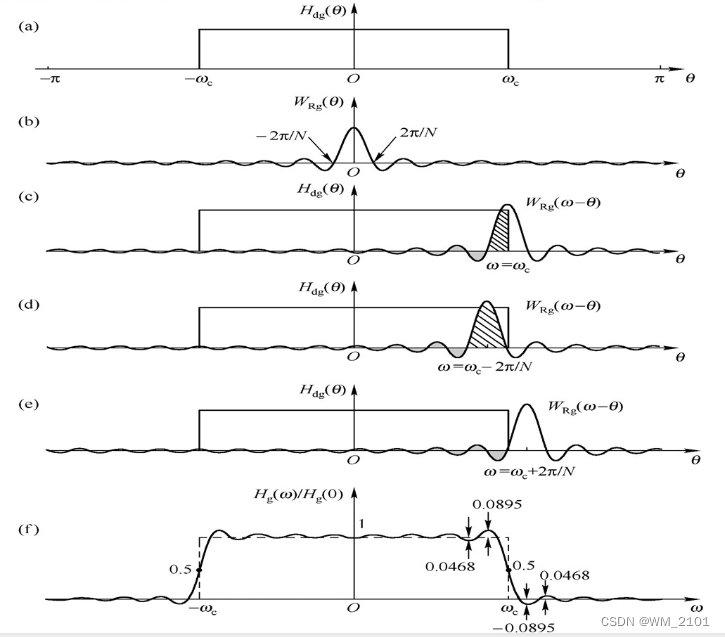
以矩形窗为例，参考教材图7.2.3，分析加窗效应的原理和结果。主瓣宽度、吉布斯效应的影响

卷积：一个函数与另外一个函数翻转平移，将抽样函数进行翻转平移，相乘求积分

主瓣宽度：是4π/N,主瓣宽度与N成反比

（c）当抽样函数中线在窗函数右边界时，卷积的结果是0.5，这个0.5不是一个近似，而是精确值，

因为它是离散信号，离散信号的频谱是以2π为周期的，超过2π的部分会叠加到下一个周期，

（d）对照（f）为峰值情况

（e）对照（f）为谷值情况

吉布斯效应：

在w=wc处形成过渡带，宽度为4π/N

波动频率随着N的增加而增大

结果的最大值和最小值的大小与N无关，导致用此方式设计滤波器时，通带/阻带的衰减是无法控制的

3、窗函数长度与加窗效应

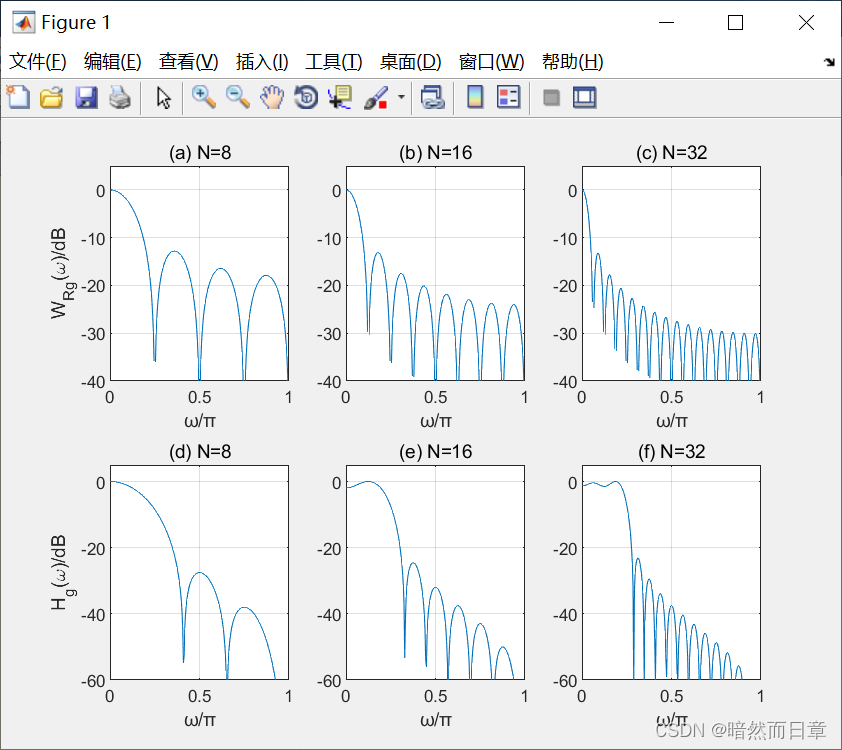
基于MATLAB，画出长度N分别为8、16、32的矩形窗函数的幅度谱，并画出基于矩形窗所设计的相应长度线性相位FIR低通滤波器的幅频响应。根据结果，总结分析滤波器长度N对阻带衰减、过渡带宽度的影响。

代码如下：

%%      代码：
close all;
wc=1/4;
N=8;
alph=(N-1)/2;
wrn=boxcar(N);              %用boxcar函数产生一个矩形窗函数
WRg=fft(wrn,512);           %对矩形窗函数进行快速傅里叶变换
hn=fir1(N-1,wc,boxcar(N));
Hg=fft(hn,512)
Hk=fft(hn,512);
w=(0:511)*2*pi/512;
subplot(2,3,1)
plot(w/pi,20*log10(abs(WRg)/max(abs(WRg))))     %画出窗函数的频域幅度波形
xlabel('ω/π');
ylabel('W_R_g(\omega)/dB')              %学一下怎么写下标和希腊字母
title('(a) N=8')
axis([0,1,-40,5])
grid on;
subplot(2,3,4)
plot(w/pi,20*log10(abs(Hg)/max(abs(Hg))))
xlabel('ω/π');
ylabel('H_g(\omega)/dB')
title('(d) N=8')
axis([0,1,-60,5])
grid on;
N=16;
alph=(N-1)/2;
wrn=boxcar(N);
WRg=fft(wrn,512);
hn=fir1(N-1,wc,boxcar(N));
Hg=fft(hn,512)
Hk=fft(hn,512);
w=(0:511)*2*pi/512;
subplot(2,3,2)
plot(w/pi,20*log10(abs(WRg)/max(abs(WRg))))
xlabel('ω/π');
title('(b) N=16')
axis([0,1,-40,5])
grid on;
subplot(2,3,5)
plot(w/pi,20*log10(abs(Hg)/max(abs(Hg))))
xlabel('ω/π');
title('(e) N=16')
axis([0,1,-60,5])
grid on;
N=32;
alph=(N-1)/2;
wrn=boxcar(N);
WRg=fft(wrn,512);
hn=fir1(N-1,wc,boxcar(N));
Hg=fft(hn,512)
Hk=fft(hn,512);
w=(0:511)*2*pi/512;
subplot(2,3,3)
plot(w/pi,20*log10(abs(WRg)/max(abs(WRg))))
xlabel('ω/π');
title('(c) N=32')
axis([0,1,-40,5])
grid on;
subplot(2,3,6)
plot(w/pi,20*log10(abs(Hg)/max(abs(Hg))))
xlabel('ω/π');
title('(f) N=32')
axis([0,1,-60,5])
grid on;

运行结果：

由图分析可知，N越大，过渡带宽度越窄，阻带衰减不变。

4、matlab实现不同窗函数设计FIR高通滤波器

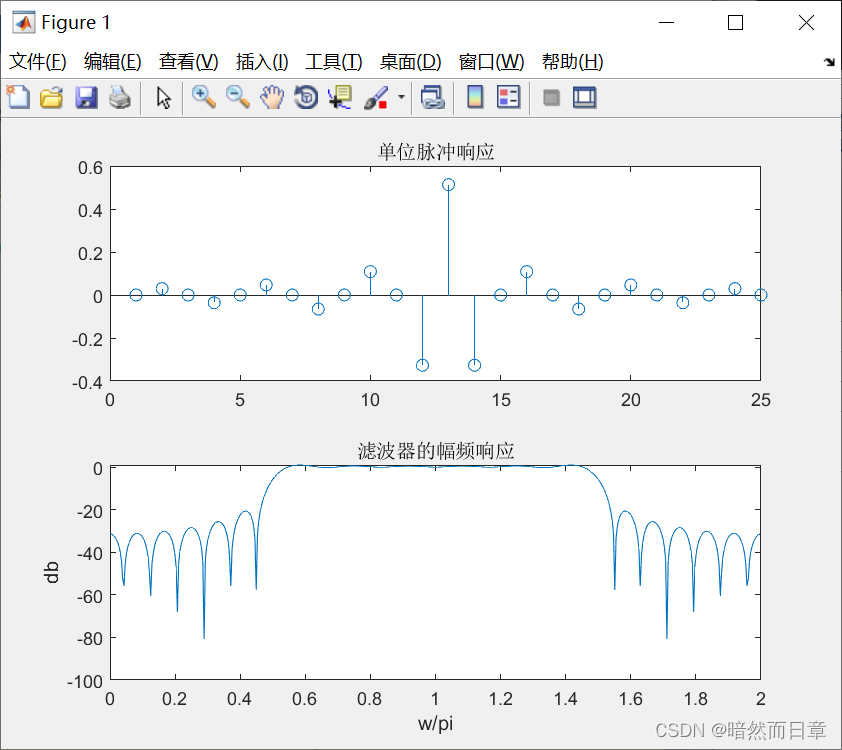
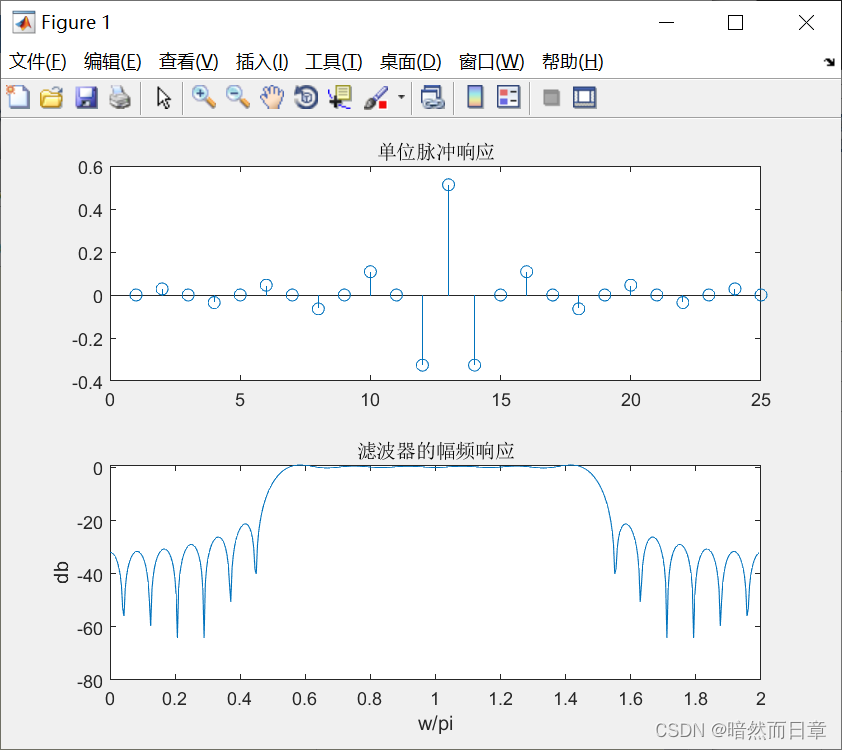
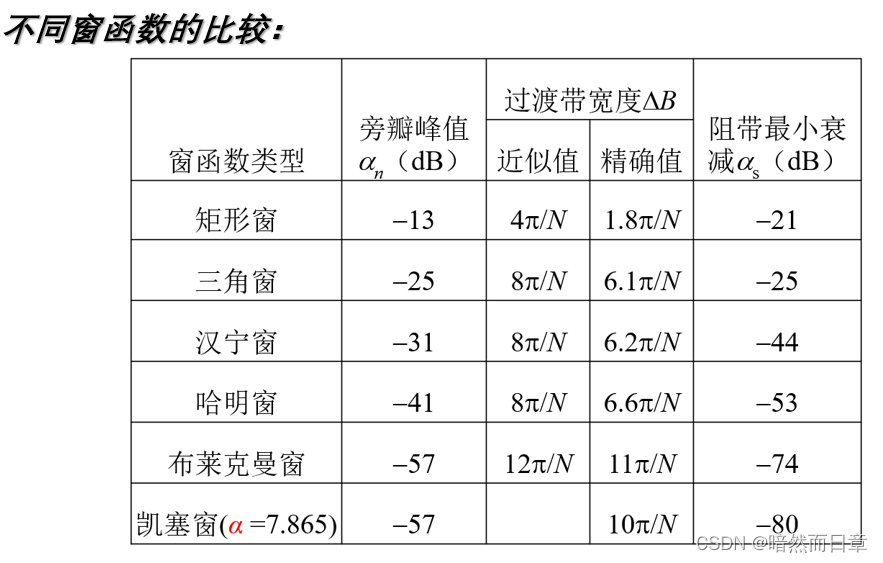
自行设定一个固定的滤波器长度N，基于Matlab分别用不同的窗函数设计FIR线性相位高通滤波器（利用fir1函数），画出所设计滤波器的单位响应h(n)和幅频特性。根据所得结果，结合教材表7.2.2，总结各种窗函数的特性和参数。与教材给出的各种窗函数所设计的低通滤波器的单位响应进行比较，比较高通和低通FIR线性相位滤波器时域响应的不同特点。

代码如下：

clear
N=25;
wc=0.5;
window = boxcar(N);     %矩形窗
% window = bartlett(N); %三角窗
%window = hanning(N);   %汉宁窗
%window = hamming(N);   %哈明窗
%window = blackman(N);  %布莱克曼窗
%window = kaiser(N);    %凯塞窗
hn=fir1(N-1,wc,'high',window);
subplot(2,1,1)
stem(hn)
title('单位脉冲响应')
subplot(2,1,2)
Hn=fft(hn,512);
Hn=Hn';
plot((0:length(Hn)-1)/length(Hn)*2,20*log10(abs(Hn)))
title('滤波器的幅频响应')
xlabel('w/pi')
ylabel('db')

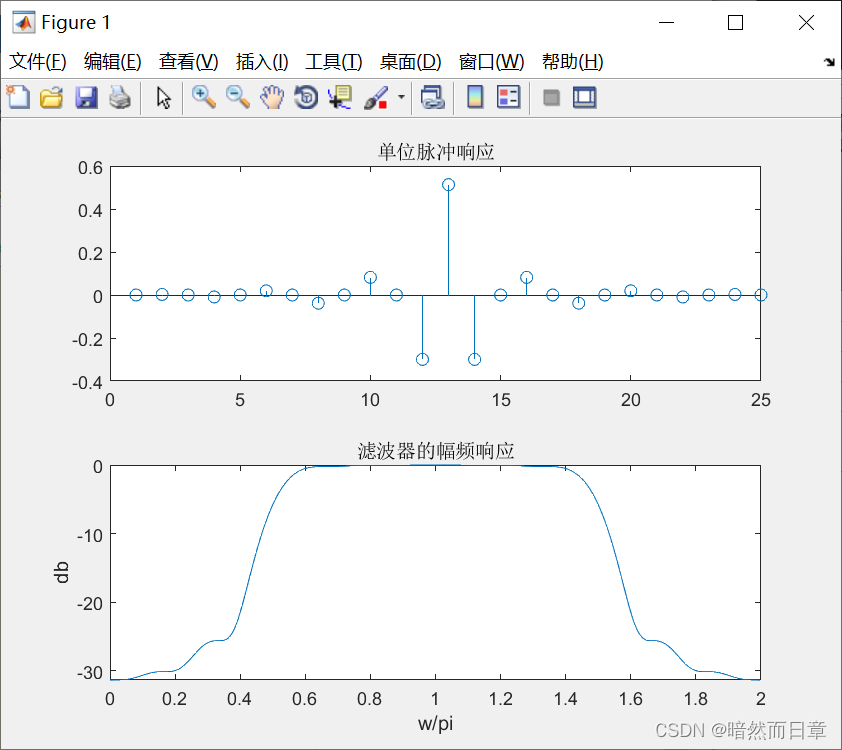
矩形窗：

三角窗：

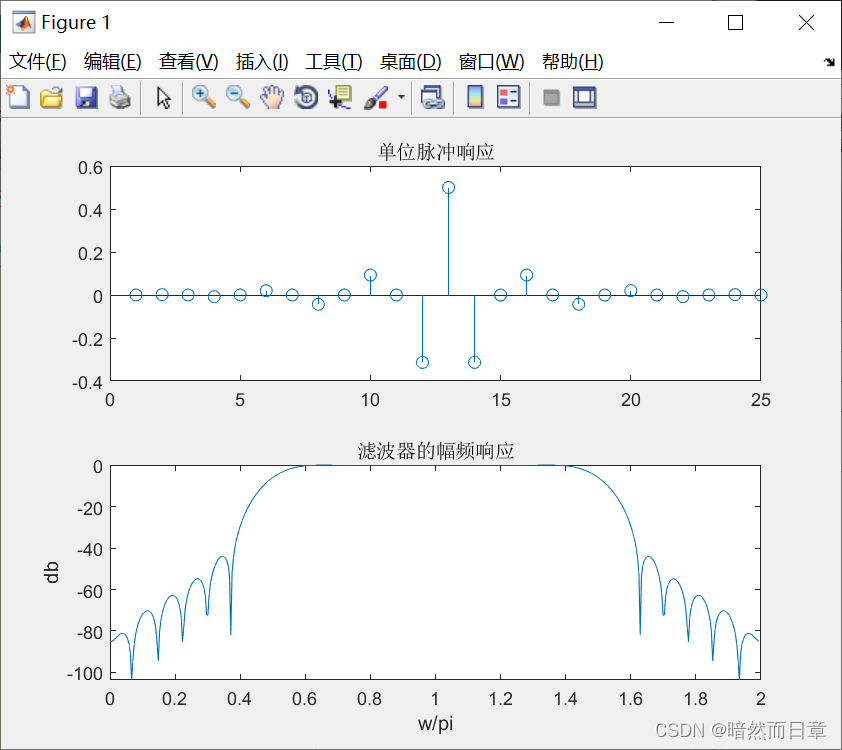
汉宁窗：

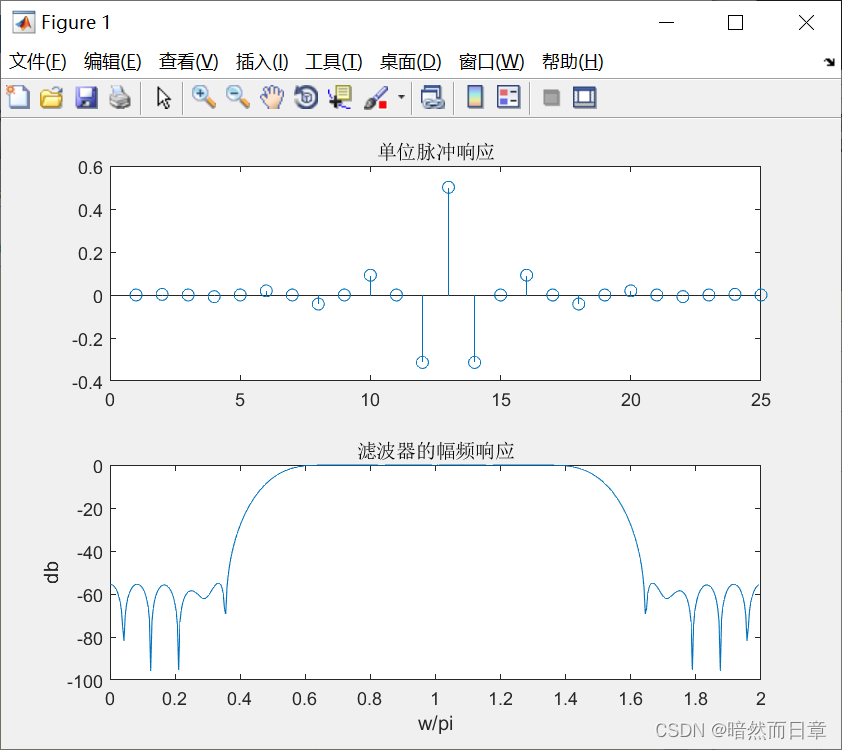
哈明窗：

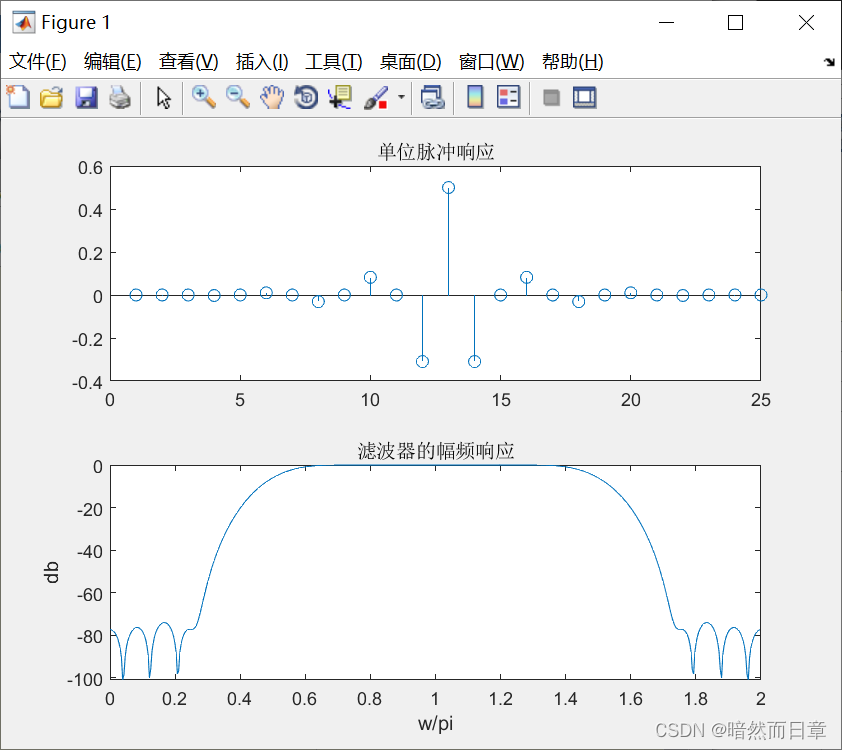
布莱克曼窗：

凯塞窗：

低通滤波器在N/2两侧的相邻两点为正值，高通滤波器在N/2两侧的相邻两点为负值。

5、窗函数法设计FIR线性相位滤波器的步骤

举例说明窗函数法设计FIR线性相位滤波器的步骤：自行给定滤波器类型和技术指标，利用窗函数法设计FIR线性相位滤波器，按照设计步骤手算（不用MATLAB编程）。

6、用matlab设计一个FIR滤波器和一个IIR滤波器并滤波

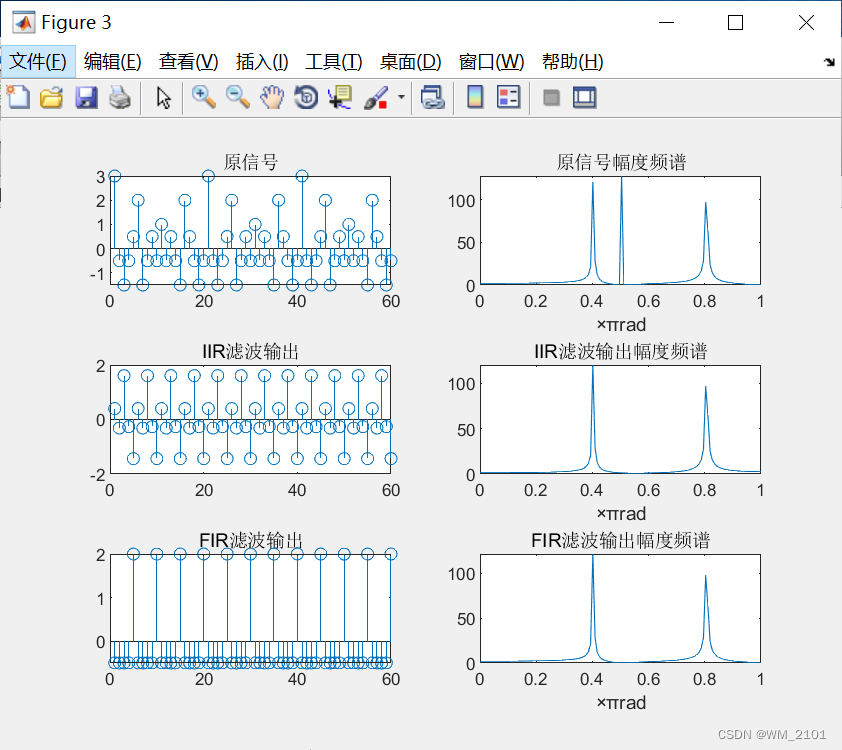
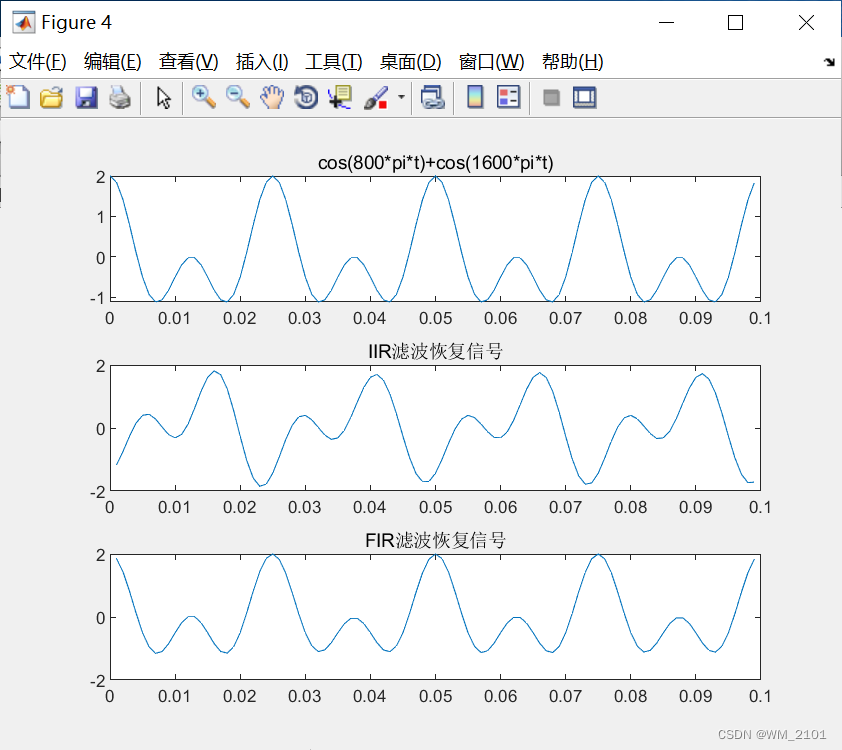
设模拟信号x(t)=cos(800πt)+ cos(1000πt)+ cos(1600πt)，用2000Hz的采样频率对其数字化，得到相应的序列x(n)。分别设计IIR滤波器和FIR滤波器（窗函数法），对x(n)进行滤波，要求滤除其中的cos(1000πt)分量（衰减到原幅度的1%以下），且保留的两个频率分量幅度变化不超过1%。a) 请根据以上要求，确定数字滤波器的类型和技术指标参数，完成滤波器设计，并画出所设计IIR、FIR数字滤波器的幅频特性和相频特性、x(n)经过两种滤波器滤波前后的时域信号及其幅度频谱，比较其结果的异同并分析其原因。b) 设x1(t)由所保留的2个分量构成（x(t)=cos(800πt) + cos(1600πt)），y(n)是IIR滤波后的输出，yf(n)是FIR滤波后的输出，利用实验一的方法，对y(n)和yf(n)进行时域恢复，恢复结果分别为y(t)和yf(t)，分别画出x1(t)、y(t)和yf(t)，比较分析其异同，总结线性相位滤波器的优点。

代码：

%%      代码：
clear
T=1/2000;
n=0:500;
t=n*T;
N=256;
x=cos(800*pi*t)+cos(1000*pi*t)+cos(1600*pi*t);
X=fft(x(1:256),N);
%%      IIR滤波器设计
fpl=800*T;                  %技术指标
fsl=950*T;
fsu=1050*T;
fpu=1200*T;
wp=[fpl,fpu];
ws=[fsl,fsu]
rp=0.083;                   %衰减不大于？？？
rs=40;                      %衰减不小于？？？
[Nf,wc]=buttord (wp,ws,rp,rs)
[B,A]=butter(Nf,wc,'stop')
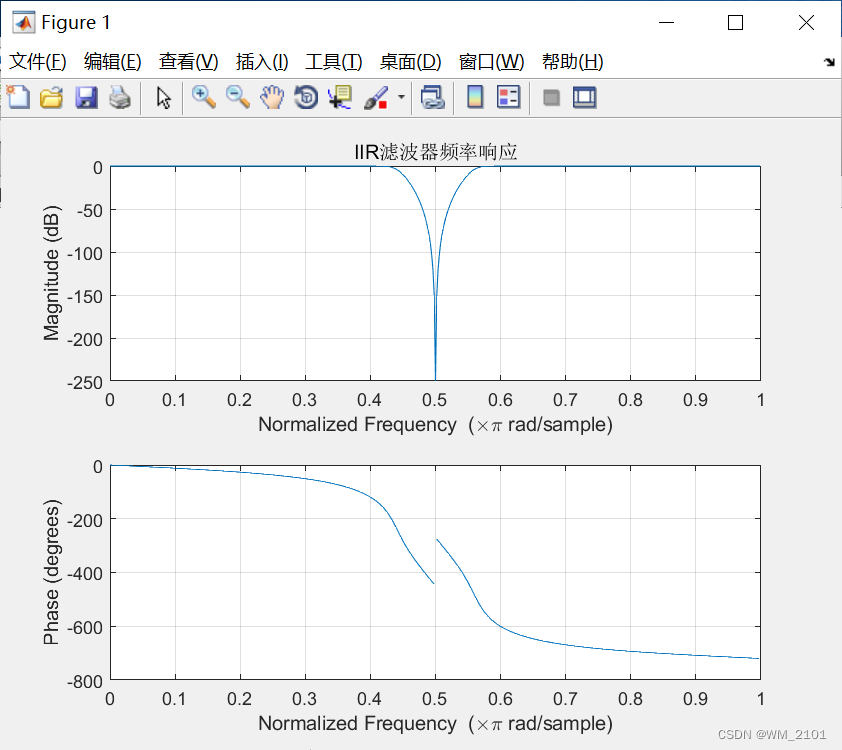
figure(1)
freqz(B,A)
title('IIR滤波器频率响应');
%%      FIR滤波器设计
Bt=fpu-fpl;
M0=ceil(6.2*pi/Bt);
M=M0+mod(M0+1,2);
Wc=[900*T 1300*T];
hn=fir1(M-1,Wc,'stop',hanning(M));      %汉宁窗
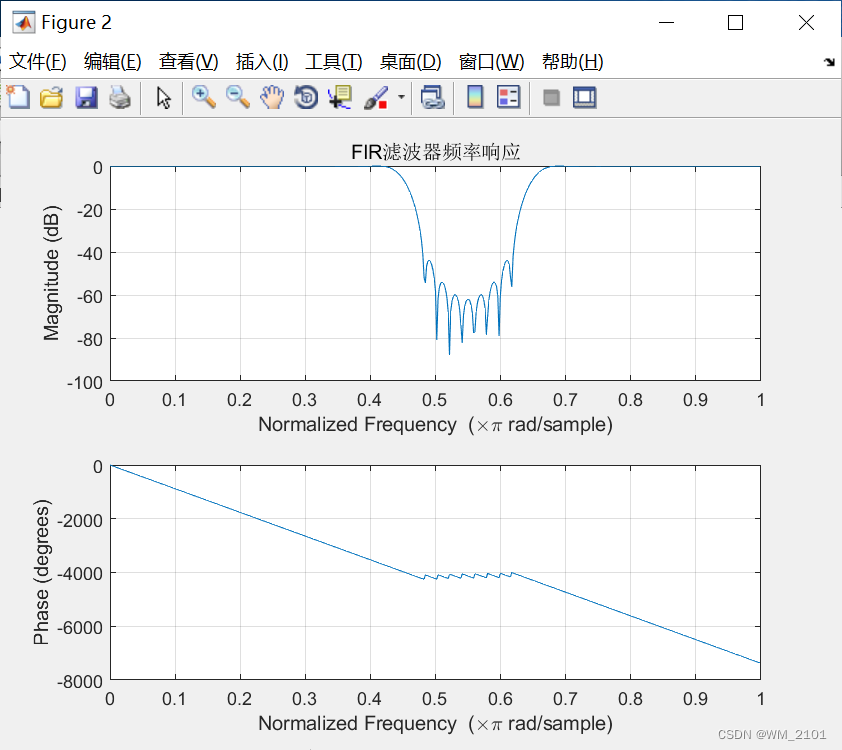
figure(2)
A1=[1,zeros(1,M-1)];
freqz(hn,A1)
title('FIR滤波器频率响应');
%滤波及结果
y=filter(B,A,x)
Y=fft(y(240:495),256);
yf=filter(hn,A1,x);
Yf=fft(yf(240:495),256);
figure(3)
subplot(3,2,1)
stem(x(301:360));
title('原信号');
subplot(3,2,3)
stem(y(301:360));
title('IIR滤波输出');
subplot(3,2,5)
stem(yf(301:360));
title('FIR滤波输出');
subplot(3,2,2)
plot((0:127)/127,abs(X(1:128)))
title('原信号幅度频谱');
xlabel('×πrad')
subplot(3,2,4)
plot((0:127)/127,abs(Y(1:128)))
title('IIR滤波输出幅度频谱');
xlabel('×πrad')
subplot(3,2,6)
plot((0:127)/127,abs(Yf(1:128)))
title('FIR滤波输出幅度频谱');
xlabel('×πrad')
t1=-0.1:0.0001:0.1;
x1=cos(800*pi*t1)+cos(1600*pi*t1);
y1=y(300:363);
yf1=yf(300:363);
figure(4)
subplot(3,1,1)
plot((0:0.001:0.099),x1(1001:1100))
title('cos(800*pi*t)+cos(1600*pi*t)');
xt=0;
for n=1:length(y1)
sc=sin(pi*(t1-(n-1)*T)/T)./(pi*(t1-(n-1)*T));
xt=xt+T*y1(n)*sc;
end;
xtf=0;
for n=1:length(yf1)
sc=sin(pi*(t1-(n-1)*T)/T)./(pi*(t1-(n-1)*T));
xtf=xtf+T*yf1(n)*sc;
end;
subplot(3,1,2)
plot((0:0.001:0.099),xt(1001:1100))
axis([0,0.1,-2,2])
title('IIR滤波恢复信号');
subplot(3,1,3)
plot((0:0.001:0.099),xtf(1001:1100))
axis([0,0.1,-2,2])
title('FIR滤波恢复信号');

运行结果：