计数排序（Counting Sort）

• 计数排序是一个非基于比较的排序算法，该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时，快于任何比较排序算法。
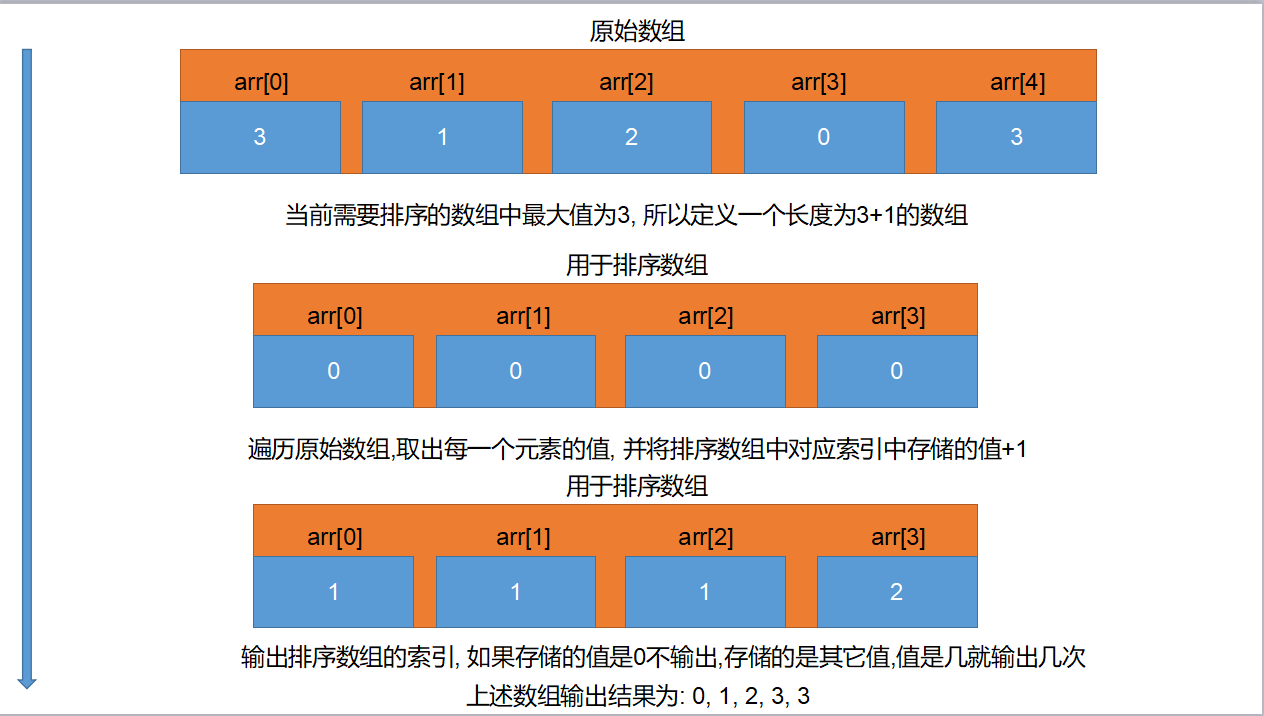
• 排序思路:
  • 1.找出待排序数组最大值
  • 2.定义一个索引最大值为待排序数组最大值的数组
  • 3.遍历待排序数组, 将待排序数组遍历到的值作新数组索引
  • 4.在新数组对应索引存储值原有基础上+1

    

    • 简单代码实现:

      int main()
      {
          // 待排序数组
          int nums[5] = {3, 1, 2, 0, 3};
          // 用于排序数组
          int newNums[4] = {0};
          // 计算待排序数组长度
          int len = sizeof(nums) / sizeof(nums[0]);
          // 遍历待排序数组
          for(int i = 0; i < len; i++){
              // 取出待排序数组当前值
              int index = nums[i];
              // 将待排序数组当前值作为排序数组索引
              // 将用于排序数组对应索引原有值+1
              newNums[index] = newNums[index] +1;
          }
          
          // 计算待排序数组长度
          int len2 = sizeof(newNums) / sizeof(newNums[0]);
          // 输出排序数组索引, 就是排序之后结果
          for(int i = 0; i < len2; i++){
              for(int j = 0; j < newNums[i]; j++){
                  printf("%i\n", i);
              }
          }
          /*
          // 计算待排序数组长度
          int len2 = sizeof(newNums) / sizeof(newNums[0]);
          // 还原排序结果到待排序数组
          for(int i = 0; i < len2; i++){
              int index = 0;
              for(int i = 0; i < len; i++){
                  for(int j = 0; j < newNums[i]; j++){
                      nums[index++] = i;
                  }
              }
          }
          */
          return 0;
      }